Capital-efficient AMM LPs generally lose money, and have done so since they began in 2021. The most prominent solutions, however, are dominated by things that have been tried: volatility-based fees, oracles, single-sided liquidity, auctions, self-financing trades, rehypothecation, options, and token rewards. It could be that these attempts are like Edison’s search for an economically viable light bulb filament, where he did trial-and-error on thousands of candidates until finding one that worked (carbonized bamboo!). More probably, it’s like the delusion that real socialism has never been tried.
The solution presented here is based on offering whitelisted arbitrageurs zero-fee trading and leverage for both the LPs and arbitrageurs. Margin trading is not only capital-efficient, but the peculiar nature of the AMM creates a clear complementary collateral relationship between arb and LP token changes. The Uni v2 AMM is used to make it easier (feasible?) to allocate arb profits to the LPs, and giving the LPs leverage can make them capital efficient while avoiding v3’s race to the bottom in liquidity provision.
Below, I outline the primary mechanisms required. The gist was discussed in the latter part of the paper I posted on the SSRN (see here), but this post provides more details, including a Python program (here) that simulates the effects of this mechanism on LP and arb profitability over random price paths —the same one I used to generate several of the charts below. It's not a comprehensive outline, as I am presenting the LP collective with a representative single LP; however, the straightforward adjustments needed to extend it to several LPs are a distraction at this point. I also have a YouTube video (here) that walks you through the simulation program and shows how the Python program’s output can be interpreted via a downloadable spreadsheet (here).
Arbs get zero-fee trading in margin accounts, taxed at 90%
Tax rates exceeding 50% are rare due to the Laffer curve. Wealthy individuals can and will relocate their assets to where they can generate better after-tax returns. However, many hedge funds pay their portfolio managers (PMs) only 10% of the PM's total profits. This is because the hedge fund offers various Prime Broker services that require scale, providing the trader with access to better financing and shorting opportunities. Most importantly, it gives the PM capital. Getting 10% on a book with a $1 billion notional is much better than making 100% on a book with only $100,000. However, the comparison is made significantly different because an AMM arb's job requires no secret strategy, just API competence. There are thousands of people worldwide who can create a simple arbitrage bot. While only a handful are good enough to generate the dominance needed to make arbing an AMM pool worthwhile, this is relative. With thousands of willing and able arbs, one can be sure that someone will be willing and able to update the AMM as an oracle would. Unlike an oracle, these price setters are pseudonymous and uncensorable.
To see the feasibility of this, assume that the volatility of a token is 4% daily. This translates to an annualized volatility of 76%. The v2 IL on such a pool is 0.76^2/8, or 7.3%. If the arb gets 10%, that's 0.73% of v2's pool market cap. The arb needs capital to trade an extreme day, say a 10% price movement. This would require an inflow of 5% of one of the tokens. If the arb showed up with 5% of both tokens, their capital would be only 5% of the v2 pool's market cap. The return on capital would then be 0.73% * 20 or 15%.
This pro forma arb APY is attractive, but it’s a lower bound. An arb should also make money off noise traders, and these profitable trades are not reflected in the LP’s IL. For example, if the CEX and DEX prices are 100, but a noise trader pushes the DEX price to 101, the arb will profit by pushing the DEX price from 101 back to 100. It’s common to neglect the effect of stupid trades on a market maker’s pnl, but they are often significant. Further, with a v2 structure, outsiders will not capture the vig from these transactions.
Further, with leverage, the arbs do not need 5% of v2 LP capital. Giving the arbs 5:1 leverage takes that down to 1% of v2 LP capital. Thus, we multiply the 0.73% of v2 capital as the arb profit from just IL and multiply this by 100, generating a 73% APY.
We can also add the reduced off-contract trading costs. By periodically swapping the LP and arb net collateral, we reduce the amount of trading the arb needs to do to adjust their accounts.
Other rules can help the arbs maximize their profits, namely, arb gas price limits and minimum price impact requirements. A gas price war is bad for the arbs; it's just a deadweight loss to the AMM going to sequencers. Minimum trade size requirements prevent another type of ruinous competition. If the arbs compete to trade on every AMM/CEX deviation with a 0.001 basis point deviation, their total profits will be zero. However, if you constrain their minimum trade size to a 3 or 5 basis point move, the arbs can prevent such 'perfect' competition.
Leverage
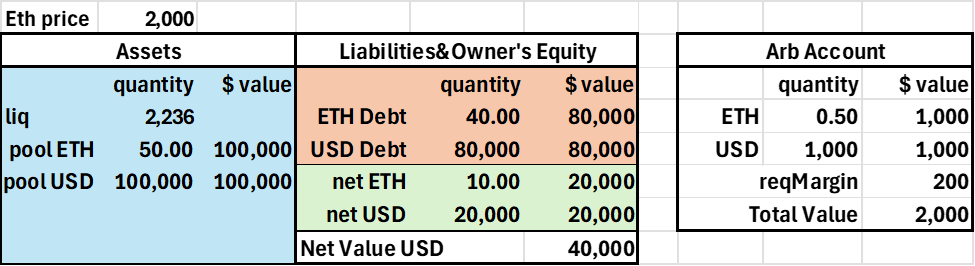
Below is an LP account levered at 5:1. When initiated, the LP's pool position is 5 times his deposit amount, creating a debt equal to 4/5 of his pool position. As the price changes, his pool quantities change, but his debt amounts are constant. The LP's net position, representing real tokens, is the difference between its assets and debt. For the arb, he deposits like for a v2 LP, with equal value amounts of both tokens (I will use ETH and USD below, but these examples generalize to any tokens A and B). The arb is bound by a simple margin requirement of 20% of the absolute ETH position, so in the example below, with $1000 worth of ETH, the arb's total value needs to be at least $200. Both accounts are maintained on contract.
Table 1
Initial Levered LP and Arb Accounts
It is helpful to represent the non-arb swappers as 'noise' traders. This does not mean they are irrational; merely that they are not generally trading on CEX-AMM price disparities that motivate arbitrageurs. For example, when Warren Buffett adjusts his portfolio, it is for long-term reasons that generate significant alpha. However, when these trades hit the exchange, they are considered noise because they are irrelevant to the short-term horizon of market makers and arbitrageurs. Of course, most noise traders have no alpha at all, and many are simply buying to invest excess savings or need cash to buy a car.
The key to noise traders is that over longer windows, such as days and weeks, their aggregate net demand is uncorrelated with the price change. This makes it reasonable to presume that the arb and LP collective's portfolio token changes are mirror images of each other. That's not true on a day-to-day basis, but it's a good approximation.
Table 2
Complementary LP and Arb Token Changes
For standard financial accounts, the primary risk is bankruptcy. For a levered v2 position, the LP's valuation function changes from being linear in the square root of price to a humped function that becomes negative at equidistant log price changes.
Thus, for a leverage of 5, bankruptcy boundaries for the LP are at -75% and +300%. This is shown in the chart below.
Chart 1
LP Value: v2 vs. Levered v2
For the leveraged LP, the primary risk to the contract is not LP bankruptcy but solvency. The AMM needs positive amounts of both tokens at all times, and these points are breached well before bankruptcy. The insolvency risk for the levered LP is
For leverage of 5, the LP will run out of USD and ETH at price change points of -36% and +56%. These are one-third of the bankruptcy points in log returns, which is helpful because it implies a significant safety margin for the contract’s overall net value.
Chart 3
Levered v2 LP net Token Balances
To protect the AMM from the absence of one of the tokens, the LP's liquidation trigger is based on its net token balance. If it is negative, the arb can liquidate the LP's pool position, swap their excess token for the deficit token, and take their fee out of the LP's excess token. Given its simplicity and the substantial value in the LP's account, liquidating the LP is a straightforward transaction. Note that in the table below, the LP is out of USD when the price is down 36%, as implied by the above formula.
Table 3
Price Declines 36%, Generating LP Default
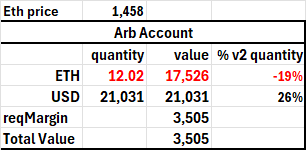
The arb's default, in contrast, is not based on token deficits, but rather on the standard required margin requirement one experiences in tradfi: the account’s value relative to the value of a risky asset. Giving the arb 5:1 leverage means they can put up 20% of the 5% of v2 tokens they would need without leverage. As a percent of v2 market value, that is 100:1 leverage. Given the arb's fee advantage, the surviving arbs will generally make a profit—the flip side of the LP's IL—so as the price changes, they should not fall below their margin requirement. Indeed, assuming the arb is the only trader, he cannot lose money. However, with decentralization, anyone can become an arb, and they can be reckless, incompetent, or unlucky.
In the example above, the price declined by 36%, driven by the arb account shorting ETH. In the table below, the arb's short ETH position would violate the 20% required margin if the price rose 14% and the arb did nothing. Unlike the LP liquidation that triggers when a minute token deficit arises, the arb's token deficit, when they have breached the margin requirement, can be orders of magnitude greater as a percentage of v2 tokens. In such cases, eliminating the token deficit cannot be handled through a simple swap on the contract, as the price impact would be absurdly wasteful (approximately 40%). A more efficient liquidation would protect the arb account, which would not merely be good for the arb but also allow the defaulting account to pay the liquidator more. An exogenous inflow of 12.02 ETH by the liquidator would eliminate the arb's deficit, and then the remaining USD would be used to pay the liquidator for the ETH and the liquidation fee. Liquidations requiring capital would generate a higher fee than those that can be processed without capital.
Table 4
Price Jumps, Inactive Arb Defaults
Arb and LP Collateral Swapping
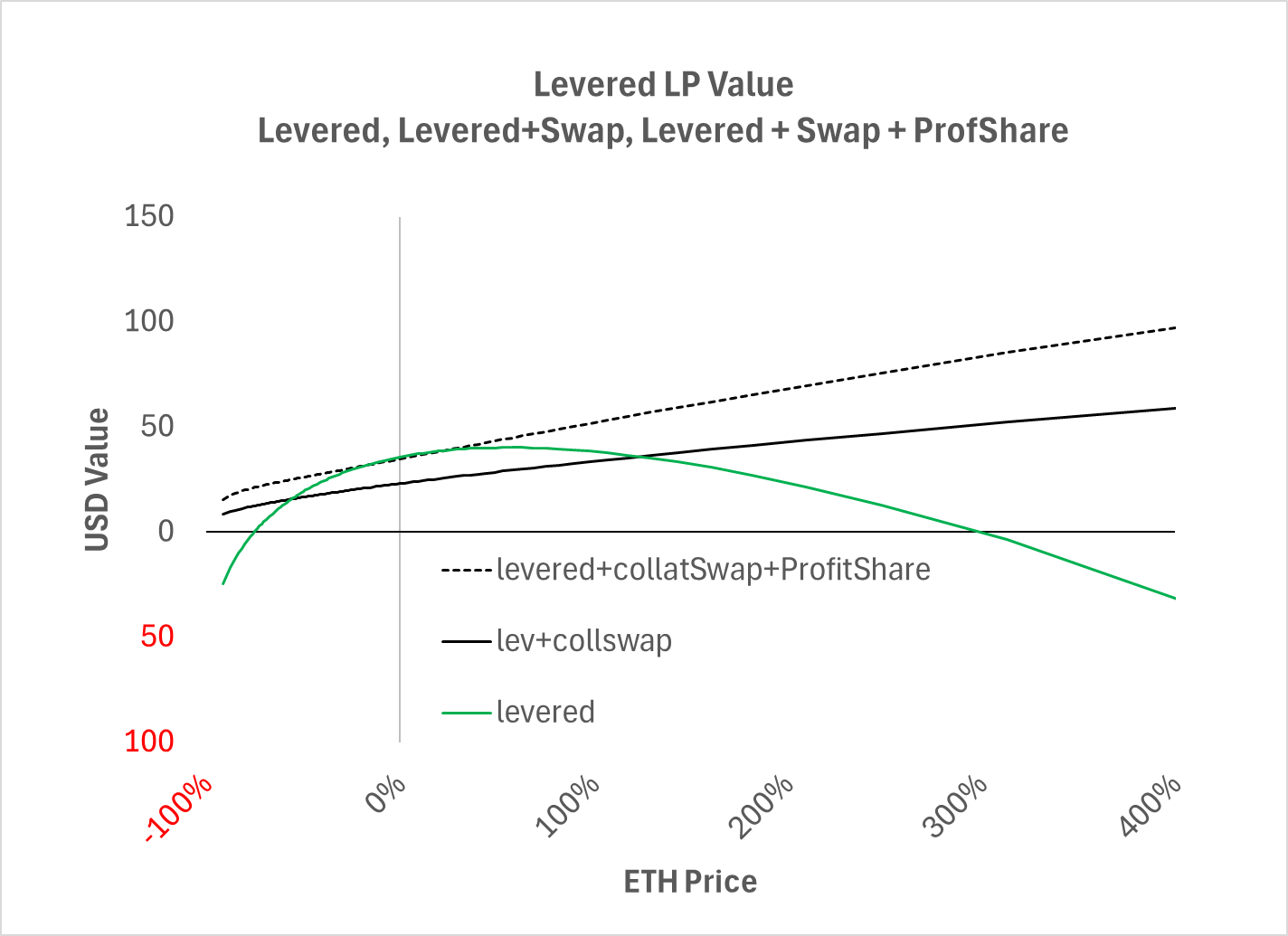
With LP and arb collateral swapping the default price points are pushed out even further, even if the arbs did not share profits with the LPs. Swapping LP and arb token imbalances eliminates the levered LP’s bankruptcy risk by effectively amortizing the LP's IL into the negative gamma expense of a hedged LP. Thus, the expected value of these two positions is the same, but with collateral swapping, less risky to the AMM and requires fewer position replacements by the LP.
Chart 3
Levered LP with Collateral Swapping
Giving the arb 5:1 leverage means they need only 1% of v2 capital to move the AMM price 10%. However, eventually the arb will need to rectify the token deficit in whatever token has strengthened. LP and arb collateral swapping addresses this problem.
Collateral swapping works as follows, using an extreme example to clarify the process. Assume the price falls by 36%, bringing the LP's net USD balance to zero.
The LP needs USD and has an excess of ETH, while the arb has the opposite. To calculate the excess ETH for each account, we take the ETH balance minus the ETH value of the USD balance.
Arb Excess ETH: (-12 – 21000/1280) / 2 = -14.25
LP Excess ETH = (22.5 – 0)/2 = +11.25
We use the smaller number in absolute value to avoid whipsawing an account from a deficit to a surplus via this method. Thus, in this example, we transfer 11.25 ETH from the LP to the arb via the LP's debt balance; taking ETH away from the LP is equivalent to increasing its debt.
For the USD transfer, we value the 11.25 ETH at the post-transaction price and send that USD amount from the arb's account to reduce the LP's debt. The net result is as follows.
Note that now the LP is squared up again, with equal values of net ETH and USD. The arb still has an ETH deficit, but not as extreme as before. The value of these two accounts is unaffected by the transfer. This is how we transform the basic levered LP curve, which implicitly shows gamma in the curvature, into nearly a straight line shifted downward, reflecting the IL realization that would occur during the transfers.
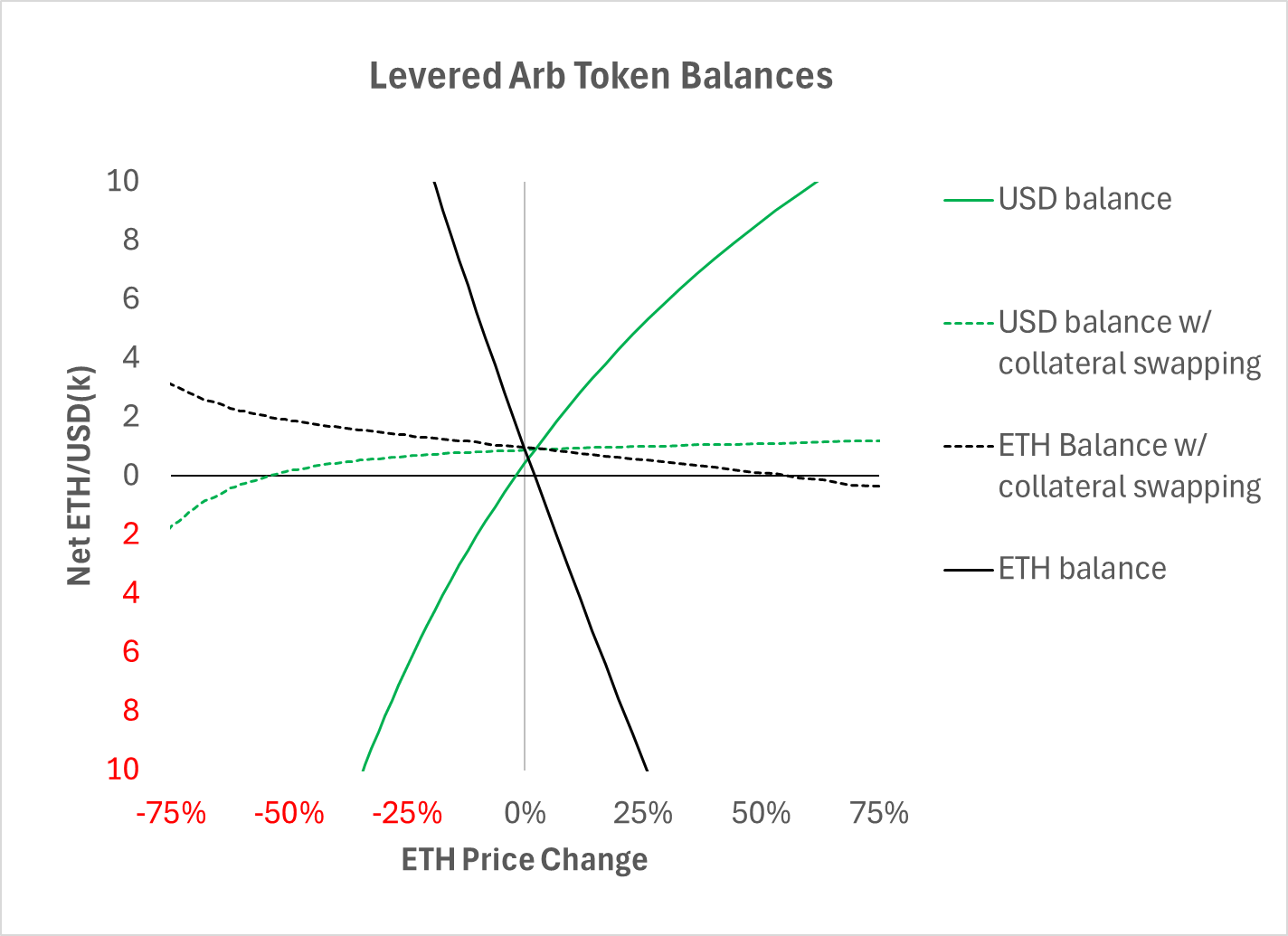
LP token insolvency is reduced from something that happens once every month to once a year via an improbable sequence of events. For the arb with 1% of v2 capital, a mere 2% price movement would generate a negative token balance. With collateral swapping, these events are pushed to 55% price movements. Furthermore, without the collateral swapping, the arb’s deficit in one of the tokens would be orders of magnitude higher, implying significantly higher capital and trading costs.
Chart 4
Levered Arb Net Token Balances With and Without Collateral Swap
Collateral swapping for the arbs is not as complete a solution as for the levered LPs, but some party needs to bring in additional tokens on extreme price movements, and as the arbs are more active, the marginal cost of shouldering this burden is better done by the arbs. In sum, the two criteria for an arb/LP collateral swap are
1) A significant token imbalance. In the simulation program, I used the LP's ETH excess being greater than 1% of the pool's v2 ETH amount. If this number is too high, the infrequency of transfer would generate greater lumpiness in the LP's net balances over price changes. If there were no threshold, the arb could game the system, moving the price up and down repeatedly, capturing 10% of the fake profits they generated on each price move (there’s no oracle, so the end-of-trade AMM price is the ‘true price’).
2) The LP's net ETH excess should have the opposite sign to the arb's ETH excess. As arbitrageurs open their accounts at various times, some may have an ETH surplus, while others may have a deficit. The transfer is driven by the arb’s trade or exit, so it would check the relevant arb account for these events. We do not want to remove ETH from an arb that already has an ETH deficit relative to USD.
These rebalancings are ideal times to apply the profit-sharing formula to the arbitrage account. For this, we calculate the arb's profit, and if it is negative, we do not take anything from the arb. If the arb profit is positive, we take the profit out of whichever token the arb has an excess of. This token amount is then sent to the LP as if it were fee revenue. We then reset the arb's account value benchmark to capture his future profit.
The profit tax would also be applied at LP withdrawal.
Thus, when everything is applied: leverage, swapping with arb collateral, and the profit sharing, the LP’s position becomes more attractive on every dimension: lower risk to the contract from bankruptcy, and an expected value reflecting a mere 10% of the IL. The LPs still need noise traders to make this profitable, but they have a much smaller hole to dig out of.