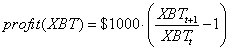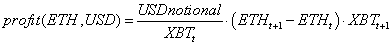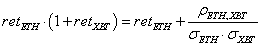BitMex's ETHUSD Funding Rate Anomaly
The high funding rates are a convexity adjustment
The average funding rate paid by long ETH swap holders has been 63% annualized since it started trading in August 2018, considerably higher than BitMex’s BTC swap rate of 6%. You can go long ETH, short the BitMEX ETH perpetual swap, and make 63% annualized on a flat book. You might need 20% down on your perp, so 63% divided by 1.2, but that’s still a nice risk-free return.
Actually, that doesn’t work for anyone interested in their USD return. This funding rate anomaly is just the result of the parochial pricing algorithm, which generates a convoluted payout.
BitMex’s large ETH swap funding rate results from the fact that payments are denominated in BTC, which is highly correlated with ETH. Adjusting the funding rate for the positive BTC~ETH covariance adds convexity to the long ETHUSD swap return. The swap funding rate for ETH adjusts for this, leaving a net funding rate near zero. BitMEX makes enough money via standard trading and liquidations, so they explicitly direct their market makers to break even over time.
The ETHUSD funding rate is like the convexity adjustment in Eurodollar futures needed to compare them with Eurodollar interest rate swap rates. In the case of futures vs. swaps, the subtle difference comes from the fact that the futures pay out their pnl each quarter while the swaps accrue it, and the payout is correlated with interest rates that accrue on that pnl. Similarly, when the long ETH position pays off bitcoin, the value of that bitcoin will tend to be higher. The Eurodollar futures-swap convexity adjustment became well-publicized in the mid-90s, but for a good five years, several large players made millions on this arbitrage (you could not make money off it without institutional access to cross margin). As Eurodollars are one of the largest markets in the world, it is understandable that a large market like the ETHUSD could also miss this adjustment.
BTC Swap Payoff
Let us first look at the profit generated by the asset price for a perp without this adjustment, the BTC perp. The long USD profit is generated in BTC as follows for an entry price at time t, and exit at t+1:
[BitMex uses the XBT for BTC. Whatevs]. As you are getting paid in BTC, and the above payoff is in USD, you need to make the final adjustment of this into BTC, so you add this final price to the payoff function to put it into the return people care about:
which implies the inverted perp payoff:
Note the backward ordering of the prices, contrary to the standard case. This is because the BTC notional amount is in USD, and we have to ultimately translate that back into BTC. It looks funny but is quite straightforward in its effect. Actually, admirably clever.
ETH Swap Payoff
The BitMEX ETH swap payoff is a notional amount times the change in the USD ETH price:
This generates a BTC-denominated payoff, however, and most people care about USD. To translate into USD, we must first take USD notional and turn it into bitcoin at time t, then turn the payoff back into USD at time t+1. The round trip starts and, ends in USD
Rearranging we get
Or using net returns:
This is the return that investors care about, not the bitcoin return. If we put this into simple net USD returns we get
As the expected value of E(x*y) = covariance of x and y, we can restate this as
If we substitute the covariance using correlation and volatility metrics for ETH and XBT, we get:
Since August 2018, the annualized volatility for BTC and ETH has been 78% and 103%, respectively, with a correlation of 83%, generating a covariance adjustment that annualizes out to be about 63%. The annualized return premium of the BitMex ETH swap compared to the ETH USD return over that period: 83% vs. 149%, a difference of 66%.
BitMex returns
8/2018-6/2022
Interestingly, the average funding rate over this period was around 63%. This implies an average ETH perp premium of negative 3%, basically zero. A short ETHUSD position hedged against a long ETH position would have lost 66% in USD terms due to the convexity generated by the ETH~BTC covariance. The high funding rate for this product is an equilibrium rate that offsets this convexity adjustment, generating no arbitrage opportunity.