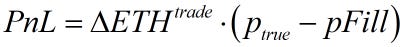In a standard centralized limit order book (CLOB), the liquidity providers (LPs) that enable instant trading at market prices are market makers that, while well-capitalized, rely on exchanges and investment banks for capital. Tradfi market making is competitive, and while those that survive generate excellent returns, that comes after much investment in hardware, software, and human capital. The passive capital providers to these market makers generally make a money market return because they have little risk, as they can liquidate the market maker if he nears insolvency.
In automated market makers (AMMs), the LPs are passive, like the lenders to TradFi market makers. An AMM pool has market prices due to arbitrageurs that act like CLOB market makers, and these arbs are few, pseudonymous, and secretive. The main problem with AMMs is that for the capital-efficient AMMs (Uniswap's v3 AMM), LPs lose money, which is why AMM growth has stagnated for over three years.
Most people acknowledge this, but it's not prominently presented to the poor LPs who put money into these AMMs, as the standard is to show only the fee revenue, like a company presenting its net income as total revenues. This ignores the costs implied by the AMM's bonding curve (e.g., the constant product AMM x*y = k). This option expense is called impermanent loss (IL), like an option's payout at maturity or its loss-vs-rebalancing (LVR), a rebranding of the Black-Scholes theta, or option decay. Hoping LPs will not notice this cost because it is variable and can be zero over various subsamples is not a sustainable solution.
An AMM can create a mechanism to capture most of its arb's profits, like proposals where arbitrageur profits are captured by forcing the arbs to compete in auctions for pool trading fees. My proposed remedy is for the AMM to whitelist arbs willing to pay most of their profit to the pool's LPs in return for trading at a discounted fee (e.g., 0 vs a standard 10 bps). The costs of running an arb-bot linked to Binance are insignificant, like that of running an oracle, as unlike TradFi arbs, they do not require the capital investment needed to generate sophisticated models and micro-second latency. The amount the whitelisted arbs should be taxed will primarily be a function of their capital requirement, and there are several ways to do this, but that’s for another post.
This approach has other essential details, but it is feasible, simpler, and more secure than auction or Oracle solutions. The bottom line is that this approach would eliminate most of the deadweight loss generated by the LP's option expense.
Many people cannot imagine how LPs can capture their pool's arb profits. They think arbitrage is between a pool and other exchanges, including centralized exchanges (CEXes) off-chain, which would make the arb’s profits challenging to capture. Below, I show that an AMM price setter, its arb, can and should generate its profits via transactions with an AMM pool ('pool' refers to a specific token pair, say bitcoin and ethereum, which generally are independent of other pools in a protocol). This makes it possible for the LPs to capture most of the arb profit via a tax applied to the on-chain position the arb acquires while servicing the pool.
Arb Profit
To highlight this solution is consistent with what AMM arbs are currently doing, first consider the arb's objective. An arbitrageur's profit is just like in traditional finance, where you multiply the amount of asset traded times the 'true' price minus the fill price for any particular transaction.
For constant product AMMs, the fill price is the geometric mean of the pool price at the beginning and end of the transaction. This implies that if an arb moves a price 1.0% to its true price, he makes a 0.5% return on that trade. Over an arbitrary period, the arb's total profits can be measured by looking at their net trades and the current market price (I like to use USD and ETH because they're easier to intuit than tokens A and B, but they generalize to any pair of tokens).
The arb's profit mirrors the LP's impermanent loss (IL), which is not a coincidence. Below are ten different algebraic representations of IL, and the arb profit is #3 (the delta signs are reversed for the LP). The cost these equations capture is the mathematical corollary of negative convexity in the AMM's bonding curve. There is no adverse selection as with CLOB market makers offering tight two-sided offers to buy and sell, and thus latency does not affect LVR/IL/theta in theory or practice.
Fees induce a straightforward adjustment to the arbitrageur's profit-maximizing objective. If the fee is, say, 5 basis points, obviously, there is no profit opportunity if the AMM pool price is 4 bps away from the true price: a gross profit of +4 bps would generate a net profit of -1 bp for the arb. When the arbitrageur pushes the price to within the fee of the true price, he is maximizing his profit.
For example, when the AMM pool price is below the true price, the arb maximizes his profit by buying until the transaction ending price equals the true price adjusted for the fee (just flip for when the AMM price is above the market price and the arb sells).
Most people envisage arbitrage as involving two legs, like when high-frequency arbitrageurs buy spot ETFs in New York and sell futures in Chicago, locking in an instant profit. This is common when the price spread jumps discontinuously at the sub-20-millisecond frequency (see chart below for arb opportunities circa 2011). At that time dimension, no exchange is leading, as the stochastic component of the exchange price will dominate; a one-day price return correlation of 1.0 between exchanges will go to zero as the return horizon goes to zero, and 10 milliseconds is very close to zero.
Any decentralized AMM will generate latency 100 times greater than CEXes with co-located servers, leading to a qualitative difference between the arbitrageur's task on DEX AMMs. For liquid coins, the CEX price pulls the AMM price around like when you take a dog on a walk, and the leash acts like the fee: you are the CEX price while the dog is the AMM price. Another big difference is that while a CEX price can change without any trade due to it being a limit order book, on an AMM, a trade is needed to move the price; price-setting arbitrageurs push the price so that if the ETH-USD price for the day is up, in general, the arbs acquire ETH from the pool. This leads to a dominant arbitrage strategy that trades primarily on the AMM, only occasionally hedging out the arb's acquired inventory on a CEX.
For example, assume a single arbitrageur trading with a pool and no fee. If the price meanders around all day and closes higher, its price path can be separated into the net rise, where the rest of the path would be a net zero for the arb (absent fees). In the graph below, one could calculate the arb's profit by isolating the first section where the price moves up to its ultimate closing price. After that, there are three sets of net-zero whipsaw movements where the average price paid on the way up equals the average fill price on the way down.
A simple local rule to follow the CEX price on the AMM—up to the fee—generates an arb profit on average. If the arb captures only 10 or 20% of the trades over a day, statistically, the arb will make money via the same logic, but on average, and almost all arbitrage is really 'stat arb.'
There are several reasons why an AMM arb should primarily trade on the AMM pool without instantly locking in a profit on another exchange. First, the relative latency of the AMM implies the CEX price leads, so all the edge in the opportunity is on the AMM, not the CEX, which would just provide a hedge. While one can negotiate explicit fees down to 1 bp on Binance, there will always be a price impact for arb trades of any significance (> $10k). A 5 bp cost, including fees and price impact, is a reasonable lower-bound estimate, as hedging is uninformed and without a high-frequency edge (AQR estimates 7 bps for liquid US equities). Innumerable failed trading strategies have been concocted using mid or closing prices in backtests. For an arb trading hundreds or a thousand times a day, that 5 bps adds up.
Periodic hedging reduces arb costs because the stochastic nature of asset prices implies that an arb's gross volume over a day will be 4 to 10 times his net position at the end of the day. He can reduce his hedging costs by 25% to 90% by exiting his acquired inventory daily instead of continuously. Consider the simple binomial tree applied to two periods below to see this. Prices can move up or down, and each move implies the arb buys or sells 5 units. Over the two periods, the arb trades 5 units each period, for a total of 10 units, regardless of where the price ends. However, the arb's net position will be +/- 10 half the time and zero the other half. Thus, instead of hedging each trade for a total of 10 units, his expected hedge amount is half that, 5, if he hedges his net position occasionally instead of continuously.
By hedging occasionally, the arb can trade multiple times with a slight edge, say 1 basis point, even though it costs him 5 bps to exit his position on Binance.
Empirical Evidence
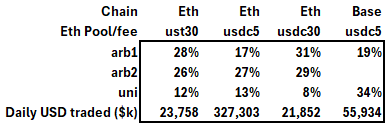
Several data points suggest this is what AMM price-setting arbs do. I looked at four different capital efficient (v3) Uniswap ETH-USD pools, three on the Ethereum mainnet and one on Base. The Base pool became very active this April when volume rose 100-fold from earlier in the year, so I started my Base pool dataset on April 22, 2024. Their current dominant arb accounts for the ETH-USD pools on the mainnet started around mid-March, so I started their data on March 15.
All these pool's LPs lose money, about $5K to $23K per day, where PnL is defined as the fee revenue minus the convexity costs (there are three ways to calculate this, and they generate similar numbers; see here). Total locked value in these pools is a noisy metric for capital, as the inactive ranges contain capital that generates no service to traders, risk or reward to LPs, irrelevant to a return on capital metric. However, the convexity costs (LVR, theta) divided by revenues provide a comparable metric across pools. These pools generate LVR about 10 to 20% greater than fee revenue, which is standard for capital-efficient pools. One can also see that the Base pool generates significantly more trades than the other pools, not merely due to its low 5 bp fee but also because the gas costs on Base are effectively zero. Thus, about 10% of Base trades are for less than $1, and 25% for less than $10, effectively test trades of no consequence (in addition to wash trading used to inflate protocol metrics).
2024 Pool Daily Averages
links to pools: usdc30, usdc5, tether30, and base5
Arb Stats
The top 5 senders to any AMM pool generate about 70% of a pool's volume. These will include front ends like Uniswap that transmit classic uninformed retail flow and those arbing the pool price (arbitrageurs will not accept the latency and fees generated by popular front ends). The current top two arb accounts for the three ETH-usd pools were the same, which makes sense because arbing them is the ultimate complementary service. Base's ETH-USDC pool only attracted dominant arbs when they became more active this spring, and recently the dominant arb left or upgraded to a new account.
BaseArbs: 0x6FBBa9…, 0x6f1FE5…
The table below shows how much of the pool’s volume the arbs generate. These two mainnet arbs generate about 50% of their pool's total volume, while my one (rotating) arb on Base generates 19%. The Uniswap front-end that directs most retail volume towards these pools is listed as a comparison. Note that one cannot directly access a v3 pool via an externally owned account, so the 'sender' to these pools is either a retail front end like Uniswap, 0x, 1inch, or various bots working through a contract. Arbs do not use the Uniswap front end because it would be costly and slow.
Arb Volume As a Percent of Total Pool Volume
Mainnet pools from 3/15/24-10/20/24, Base pool from 4/22/24-10/20/24
The arbs send more trades the lower the fee and latency, as expected.
Arb Trades per day
The table below shows the net-to-gross trade volume for various pool traders. For example, if the arb buys 100 and sells 50 over a day, his net-to-gross ratio would be 33%. It is lower for the lower-fee pools.
Average Daily Net-to-Gross Trade Volume
Given CEX prices are generally within 5 bps of each other, and tick data often vary by 5 bps even when the mid-price is stable, it's understandable the average price impact on the mainchain 5 bp pool is about 5 bps, and a slightly larger 8 bps for the 30 bp-fee pools. However, it's surprising the trade impact on Base is so low, only 1.2 bps, even though the gas costs there are effectively zero. As the profit per trade is half the price impact, the edge on these trades is between 0.6 and 4.1 bps. Since uninformed trades are costly, at least 5 basis points, they would have zero chance of profit if they hedged each trade on a CEX.
Average Price Impact per Trade (basis points)
Below is the PnL for the LP collective and the arbs I singled out, with Uniswap's front end as a comparison. For this PnL, I used end-of-day prices, effectively generating an end-of-day mark-out PnL for all the trades by these users. The LP PnL will equal the negative of all the various user PnLs. These PnLs are net of fees, and the LP includes the IL harvested by the arbs. Note that the arb PnL is greater than the LP loss, and Uniswap front-end users lose a substantial total amount (they are the RobinHood of uninformed trade flow). There are other arb accounts at work, who also make money off other traders and passive LPs.
Daily average PnL
The fact that these few arbs generate profits greater than the LP losses highlights they make money not merely from the LP's implicit option but from uninformed traders. For example, if the true price is 100.00, a noise trader moves the price down to 100.50; the arb pushes it back to 100; a noise trader pushes it to 99.5; the arb moves it back to 100.0. In that sequence, the arb profits from the buy and sell, but the LP experiences no IL because there is no net price movement. Noise traders generate fee revenue for LPs, but unlike CLOB market makers, the LPs do not capture any profits from reversing uninformed price impact. The LPs could cover their IL and access this extra profit if they owned the arbs.
AMM Arb Price Targets
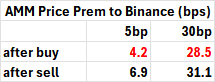
The first data supporting the hypothesis that AMM arbs target Binance is to look at the ending price for the arb transactions and match it to the Binance data downsampled to the second. Consistent with the figure above showing how a profit-maximizing trade stops at the true price plus or minus the fee, the ending price for the 0xA51 arb was within a basis point of the fee from the Binance price for the ETH-USDC 5 and 30 basis point pools.
Arb Transaction End price relative to Binance Price
AMM arbs treat the Binance price as the true price, and it's a good assumption in that, like an efficient price, its current value is the best estimate of its future value, as reflected in the future price drift
Binance price change over the next 10 seconds for Above Arb Trades
Simultaneous trades
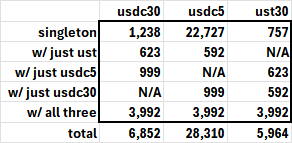
When the arb 0x51C account traded in the same block across all three pools, in 3990 out of 3992 cases, the trades were all in the same direction. This suggests a price spike on the CEXes motivated those trades. When the arb traded the 30bp fee pools, he simultaneously traded the 5bp pool most of the time, and he rarely traded a 30bp fee pool without simultaneously trading a different ETH-USD pool. This is consistent with the CEX price jumping 5 or 8 bps for a sufficient duration, say one second, implying the same trade across several AMM pools. Price discovery happens on CEXes, which the DEXes follow.
When the DEX leads, Arbs do not follow
For futures and spot markets, there's a buyer for every seller. With AMMs, there are net buyers or sellers as the LPs passively absorb excess supply and demand. For just about every originating account, their demand correlates with asset price movements. For example, below, we see the daily net ETH bought against the ETH price change for our Base arb. If the arb tends to be net long on a day that ended up, that's positive for the arb's profitability.
However, arbs are not simply looking at the CEX prices but the relative AMM-CEX price. Generally, this looks like following the CEX price because the more liquid CEXes are leading price discovery, generating more frequent trading signals. Yet, there are days when the AMM prices have led, and the reaction of the arbs to this anomaly is instructive.
For example, on August 5, 2024, the ETH price fell 15% from midnight to 3 AM GMT as some whales were dumping positions. The mainnet 5bp ETH-USDC pool fell even more quickly, generating 5% price premiums on Binance over the AMM. Even as the pool price fell like a knife, the arbs generally bought because they deferred to the CEX price. Interestingly, the second arb seemed to have lost his nerve around 1 AM GMT when the price bottomed and did nothing for the next 40 minutes. Arb 1 stood pat for the rest of this period, while arb 2 considered this a buying opportunity.
The AMM price decline implies that, in aggregate, traders were selling, which is reflected in the green line above. On average, the arbs dominate the pool’s net token changes, but in this instance, the arbs were doing the opposite. While the arbs could have lost a lot of money if the price kept falling, the price hit the floor of around $2200 until noon and then rose 10% by the end of the day. Their profit could have been anywhere between -$2 and +$5 million, depending on when they hedged. The important point is that the arbs deferred to the CEX price during this time of stress.
Asymmetric Profits
The literature on cognitive biases generates theory and data for why people under and overweight various improbable events. Nobel prize-winner Danny Kahneman's most prominent paper was on Prospect Theory, which 'explains' both. These theories do not predict, but people love them because they are useful in explaining bad data points. It is easy to understand why many DEXes and their LPs ignore IL in that, most of the time, it is insignificant, and when large losses occur, one can explain them away as anomalies, not data.
Profit-seeking crypto entrepreneurs can manipulate this cognitive bias and hope they generate enough buzz to get rich in the short run and figure out a sustainable business model later. Thus, if you exclude the worst 2% of all LP days in this sample, these four AMMs would have made a profit for their LPs. A good DEX CEO can explain those big losses away as sui generis, well enough to keep hope alive for those current LPs deluded into thinking they are getting in on the ground floor of the next Bitcoin.
The other side to the LP loss asymmetry is that AMM arbs that hedge their positions daily generate profits from 2% of their days. This is common for TradFi market makers, as a good strategy is to tread water until the next panic or hysteria arises and then make boatloads when everyone is out of their mind. Hedging daily vs. continuously reduces hedge expense by 25 to 90% for these arbs, but this comes at the cost of generating greater volatility the longer they wait to exit their inventory. However, when the asymmetric PnL is on the upside, not down, there is no big capital savings from reducing this volatility as it diversifies over time (it’s uncorrelated).
The tables below show how the LPs, arbs, and Uniswap user collective performed in three scenarios: total, worst 5 days, and best 5 days. For example, arb 0x51c made a total of $2.6MM on the ETH-USD 30bp pool, equal to the profit generated by his best 5 days. His worst 5 days cost him $375k in total. In practice, a rule based on position size and profit would be better than a simple end-of-day rule, but the gist here is that arbs have good PnL asymmetry, befitting that of one long gamma.
Conclusion
AMMs have stagnated since their initial peak in 2021 as LPs have intuited, but probably not understood, their amortized impermanent loss is greater than their fee revenue. Whitelisting arbs to give them a dominant competitive advantage and then taxing their profit is feasible and consistent with what current AMM arbs are doing, which is not 'atomic arbitrage.' As with anything, there are bad ways of doing this that would negate all the benefits. Further, there are ways to improve it by allowing the arbs to be more capital efficient. Arb capital efficiency is critical to minimizing how much you have to let them keep because capital requires a positive return. In contrast, the arb algo is almost as trivial as an oracle service and can be automated.
As the AMM arb edge is all on the AMM side, the trades are made there and occasionally hedged/exited via a liquid CEX. The LPs can thus claim their reward directly because they can access and value these on-chain tokens in the pool's numeraire.
Most Defi people don't understand gamma, and most crypto VCs are focused on convoluted incentive programs that pump their token (e.g., Aerodrome). I have thought about this for a while, so I'm available if anyone wants help implementing a system of whitelisting arbs and seizing most of their profits. I don't even want any money; I'd just love to see someone do this so I can invest in them. If you run an AMM protocol or something related to it, you need this or something better to avoid becoming the next zombie DEX. Farming, leverage, or rewards will not save AMMs that rely on continued LP ignorance.