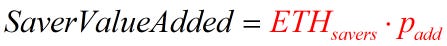Thorchain (TC) is a great protocol burdened by an endless sequence of inept innovations. Its market cap peaked in 2021 at $5B and is currently at $1B.
As it generates $70k in fees daily, that's a value protocol compared to fartcoin, which is also worth $1B and has zero fee revenue. However, like most AMMs, its net profit—fee revenue minus convexity costs—was negative in 2023 and 2024.
Like most AMMs, they don't realize their net LP profitability is negative. From TC’s website, these are standard delusional Defi performance numbers that can’t be tied to anything. Every AMM purports to generate at least 20% returns, if not 100%, excluding convexity costs because WTF is that anyway?!
The tragedy here is that this could be a valuable protocol. There will always be a need for decentralized swapping of native tokens from different chains, as some are better for privacy, storing wealth, or contracting (Monero, Bitcoin, and Base). If you always use a centralized exchange like Coinbase to transfer between them, you open up an attack surface. A malicious government can coerce them to seize your funds, as when Canada froze the banking assets for merely protesting the Covid policy. While many bridges work, they are generally centralized black boxes, not long-run solutions. TC is an AMM where you can swap ETH for BTC, not 'wrapped' BTC, all at a fair price. It isn't fully decentralized yet, but unlike Arbitrum, Avalanche, or Hyperliquid, it has a clear path.
TC is both an AMM and an L-1 blockchain developed using the Cosmos SDK and the Tendermint consensus protocol. The AMM fee revenue has to pay both their LPs and Node operators, which is a big ask because most AMMs cannot even pay for just LPs [TC calls their LPs Dual LPs, or DLPs]. Fortunately for TC, they did not adopt the standard Uniswap v3 restricted range approach for their AMMs, so their LPs are not massively and consistently unprofitable, just barely unprofitable. Unfortunately, their unique features and reporting give them just enough breathing room to exist but not enough to force real change.
They are led by JP Thorbjornsen (JP Thor), who has the confidence and ambition of an entrepreneur parody. TC's mandarins have naïve views about the economics of AMMs and tokens, leading to a focus on complicating things. Smart people with little financial knowledge love to complicate things because it makes it easier to think their refinements’ value-add is plausible, both to themselves and outsiders; complications make criticism more difficult, and it’s easy to believe in something one doesn’t fully understand (eg, origin of life). A big problem for TC is that two-thirds of LP and node operator revenue comes from minting their own token. The fact that these minted tokens are distributed from a fixed reserve doesn't change the fact that this is pure dilution, as before distribution, these treasury shares generated no sell pressure and absorbed no fees.
A blockchain like Bitcoin mints coins for its miners, but this does not confuse the miners because they have one job. JP Thor aspires to provide an infinite array of Defi products and services. This is where Hayek’s insight on the importance of market prices and profit (The Use of Knowledge in Society) to make clear what needs to be fixed, exited, or expanded. Measuring profitability is difficult when external fee income is combined with income minted out of thin air.
For example, say TC generates fees of 10 Rune, and 20 Rune are printed in the same period for 30 Rune. The node operators and LPs split 30 Rune 50:50. Node operators bear off-chain electricity and web hosting expenses, while LPs bear the impermanent loss (IL). There's good reason to think the minted Rune is pure dilution, similar to when the Fed prints money to buy bonds from the Treasury. If that is the case, the minted Rune just redistributes the fee revenue to the node operators, but this is hidden because both parties receive minted Rune that looks the same.
There have been endless debates about whether fiat creation is purely dilutive, as in monetarist or real business cycle models, or generates a money multiplier effect, as in Keynesian models or the new MMT theory. Following Satoshi's white paper, the crypto community should be biased towards a hard-money stance, viewing printed money as a tool of mischief and confusion. Hard money lowers ambiguity and allows for more efficient decisions. Unfortunately, it's tempting to print money in the short run, sowing the seeds of future crises, if not complete ruin, as with Venezuela and Luna.
The Many Missteps of TC
They use a fee model that effectively charges the end-of-trade impermanent loss, their SLIP fee model. Like the impermanent loss (IL), it charges a higher fee percentage the larger the trade. However, the per-trade IL protection model does not generalize to affect IL, let alone eliminate it.1 They soon acknowledged their fee model did not immunize LPs against IL, but kept it anyway, citing its other dubious benefits.
In October 2023, they introduced streaming swaps, which break a trade into digestible chunks so traders can avoid costly price impacts. This is like what time-weighted-average-price trades do, and these are common in tradfi because they solve a simple problem, replacing a trader manually splitting up a trade into something automated. The problem was that a significant amount of TC's fee revenue came from recklessly large trades due to their quirky SLIP fee; a regular trade may cost 5 bps, but a big trade may cost 30 basis points. The imprudent trades dominated their fee revenue.
Protecting traders from self-inflicted costs is an excellent service, like AMMs that protect traders from MEV shenanigans around imprudent large trades. However, the stupid traders were effectively subsidizing the prudent traders, and with streaming swaps, everyone got the 'below-cost' trading fee. TC fee revenue as a percent of volume, the effective fee, fell dramatically. From Nov '23 through Aug '24, their effective fee was a mere 4 basis points, compared to 12 bps before streaming swaps.
This drastic fee impact went unnoticed for several months because they allocate variable amounts of minted tokens to the LP and Nodes over time. Looking at their earnings allocated to LPs and nodes in the chart above, the nodes experienced a radical decline in earnings, making it difficult to know the root problem was in the lost revenue from the recently deleted imprudent trades. It wasn't until August '24 that TC increased the fee back to something reasonable. Even then, I doubt they realized what specifically caused their problem, as minted tokens dominate their internal profitability metrics. You cannot manage what you do not measure well.
IL Insurance
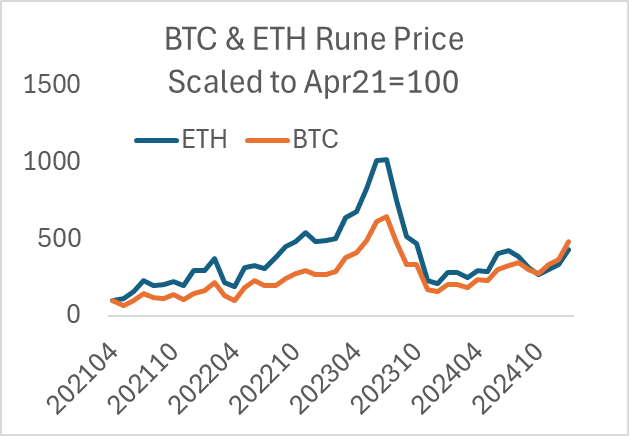
Most AMM LPs and developers do not understand IL, so providing insurance against it would be like an ardent pro-vaxxer offering insurance against vaccine side effects (why not? It’s costless). The price of Bitcoin in terms of Rune has ranged from 5k to 30k since 2021, generating significant IL at its peak in 2023. Luckily, TC stopped IL protection after the ETH and BTC Rune prices fell back from their highs at the end of 2023, but it was a close call. Continuing IL protection would ensure protocol death like what happened to Bancor, which reneged on its IL protection in 2022 and never recovered.
Single-Sided Assets (SSAs) to the Rescue
In response to the IL-protection near disaster and flagging LP growth, JP Thor had the idea that instead of fixing his AMMs to make LPs profitable, he would instead make them obsolete. The first component would be single-sided asset accounts, SSAs (TC calls them savers or synths). These add a non-Rune asset to the various Rune-asset pools. SSA deposits have zero IL risk and are paid an interest rate like a bond: you put in 1.0 BTC and get back 1.0 BTC plus interest. The second part is Protocol Owned Liquidity (PoL), which creates an LP position but is applied tactically to various pools depending on need; PoL is effectively a subset of their LPs but with a different on-ramp process. [Below I will refer to LPs, which includes PoL]
TC advocates, at times, have touted that PoL diversification across pools lowers IL via diversification, just as standard portfolio diversification lowers volatility. It doesn't work that way. IL is a linear function of variance, and diversification lowers variance. However, that is because returns cancel out, where a +2% return and a -2% return make the portfolio have a lower variance. IL is a function of the variance, the return squared. The expected value of a portfolio of independent IL risks equals the expected return of a single IL. PoL averages out the IL across pools but does nothing to lower aggregate IL. Dynamic allocation of LP funds will not improve LP performance.
This strategy only seemed attractive due to its parochial complexity, which shielded it from analysis. It avoided the fundamental problem of making LPs profitable by seemingly avoiding the need for LPs: they had PoL and Savers! As JPThor is fond of noting, everyone loves the simplicity of depositing ETH for a simple, risk-free return, and this would boost TVL and liquidity, both Key Performance Indicators.
The fact that users love simple, risk-free returns on their Bitcoin or ETH does not mean this is a good product. There are many infeasible business models that consumers would love (e.g., lottery tickets that win every time). SSA depositors like risk-free returns, but their income comes from the LPs and node operators. What is the benefit to LPs and nodes?
The effect of SSAs on the liquidity pools is two-fold. First, it reduces the LP's delta. If a saver adds 1.0 BTC to a BTC-Rune pool, half of the BTC deposited is converted to Rune, so the pool's net delta rises by that half BTC sent to the pool. However, the pool owes the saver 1.0 BTC, so the pool's net delta declines by 0.5 due to the saver deposit.
The increase in liquidity from an SSA is just a convoluted way of giving LPs leverage. The LPs do not increase their value via the SSA, as the net LP position value is unchanged. However, the pool offers traders more liquidity, lowering price impact. The SSA does not increase pool liquidity directly; it is merely used as an accounting contrivance that gives people the illusion of a direct increase in liquidity (TVL is higher!). This is evident in the fact you can generate the same increase in pool liquidity without SSAs, most obviously via a v3 approach.
I present some graphs to see how this works, but the derivation is below for those interested. Adding a 1.0 ETH SSA deposit to a pool worth 2.0 ETH is portrayed in red as a '+0.5 Savers'; the additional ETH is worth half the original pool value. An ETH deposit of equal value to the pool is labeled '+1.0 Savers.' The SSA does not change the value of the existing LP's position. The increase in virtual liquidity owned by the LP equals the increase in the LP's ETH debt.
The upward-sloping value function reflects the positive delta of an LP position, which is equal to half its value initially. Adding single-sided liquidity reduces the LP delta, reflected in the lower slope for the red and green lines at the initial add price of 3k USD. Given that TC does not provide clear information on the effect of SSAs on their various pools’ deltas anywhere, and no one besides me has ever lamented this omission on their Discord channel, their LPs are likely indifferent, if not oblivious, to the explicit delta impact of SSAs.
The single-sided addition also increases the LP's convexity, as shown in the curvature of the above lines. Adding 50% in value via an SSA increases convexity by 50%, and the 100% SSA add increases convexity by 100%. The convexity cost—expected IL, theta, and lvr—increases linearly with liquidity.
LPs could generate the same increase in liquidity (and convexity) using restricted ranges without the cost of paying for the SSAs and also save on capital. For example, a restricted range covering a price range of {750, 12k}—a -25%, +400% price change—generates the same liquidity as the +0.5 savers case and would reduce the LP's capital required by 25%. Below, the curvature, reflecting the LP’s convexity, is the same for the red and green lines. LPs would increase their return on capital in the numerator (less cost) and denominator (less capital) using restricted ranges instead of savers.
Restricted-range LPs generally lose money. This is driven by a race to the bottom among LPs who provide ever-narrower ranges to maximize their return on capital. If a protocol constrained their v3 ranges to be at least +/- 50% or higher, that problem could be avoided. If LPs do not appreciate the delta reduction from SSAs, a v3 range dominates: less cost and capital.
Conclusion
TC has a valuable protocol underneath its many clever but counterproductive attempts to add value. While TC can fix itself, that's improbable. An alternative would be for someone to copy most of their existing infrastructure with a handful of strategic changes. While this is simple, amazingly, Mayachain was a friendly TC fork that made a worse version (e.g., multiple protocol tokens, kept IL insurance).
There's $600kMM in TVL but only $200MM in the pools and $400MM for bonding their nodes. Switching to a v3 with ranges of {p/4, p*4} would reduce the pool capital required by half, or $100MM, and therefore also, the node stake required for system security could be cut in half. Thus, instead of buying TC out for $1B, you could replicate it for ten or twenty million in development and marketing costs, plus a loan of $300MM for seeding the pools and node operators.
Alternatively, one could offer the LPs leverage, facilitating a low-cost arbitrage mechanism controlled by the protocol. This approach is outlined more in a prior post here. Again, with leveraged LPs, the capital required could be cut in half, and no expense paid to SSA. This would capture most of the IL lost to arbitrageurs because, with a liquidation mechanism, the arbitrageurs could be leveraged. A modest amount of capital and access to a web-hosted account that monitors the CEX and TC pool price would be required.
Bad dapp development is the norm because so many unsustainable dapps have generated hundreds of millions in profits underlying crypto VC capital (Augur, Axie, Ohm, Perp-dot-fi, Blast, OpenSea…). Features don’t have to work; they just have to be plausible at a high level. KPIs increase when users chase rewards, which drives the token up. Ultimately, sustainability does not work, and insiders will still walk away with big bags. This ineptitude creates an opportunity, but it’s only visible to those outside the dominant crypto VC weltanschauung.
Appendix
How SSAs affect LP value and delta and gamma
LPs are pro-rata so that you can think of them as one guy, Bob.
Assume a pool with ETH valued in USDC; p is the price of ETH in USDC. His initial sensitivity to ETH's price, his delta, is
Saver Alice adds ETH to the pool at price padd, the price at the time of the SSA deposit. The value of the saver's addition is:
I will keep the ETH effect in red to clarify its impact. The effect on the pool's liquidity has increased the value of the Savers addition divided by 2*sqrt(padd). The impact on liquidity units is determined at the time of the add and does not change
ETHsavers has to be paid back, so while the amount of ETH owed is constant, its value in USDC changes (thus, pt, not the fixed padd).
The value of Bob's LP after savers is
The savers addition initially cancels out because at the inception of the single-sided addition, pt = padd. The initial savers add does not change the value of Bob's LP position at inception.
Bob's delta, in contrast, does change instantly, given the saver's addition.
Effect on gamma
If you allow SSAs for both tokens, you remove the delta effect, but then the v3 approach generates an identical convexity at half the required capital.
Firstly, note that both the 5 and 30 bp fee pools lose about the same amount of money as a percent of their total revenue, and the IL fee can be considered a variable but high fee. Arbs anticipates the fee when they trade.
Secondly, a per-trade IL protection does not scale. For example, the chart below shows a sequence of trades pushing the price by 1.0 for each trade. The beginning price is 100, ending at 101, and the next trade, the beginning is at 101, and the ending price is 102. The trader's fill price will be in the middle of a standard AMM.
The difference between the fill price and the end price is the difference between the red dot and the green dash. If the red dot represents the 'true' price, many have thought it is outrageous that traders can get a better price, noting these evil arbs are getting to trade at stale prices. However, with large price changes, you can see that the average of the green dashes and the red dots is not large. As the IL that hurts LPs tends to be on the order of at least a daily standard deviation—300+ basis points--and an arbitrage trade is generally around 10 basis points, this effect is second order. Further, the arbs respond by machine-gunning trades. For example, if the price moved from 100 to 105, charging the end-of-trade price of 105 can be avoided by generating many little trades, so the average price is around 102.5. The end-of-trade price as IL protection does not work, but it does signal a profound misunderstanding about IL.