Vertically Integrating Arbs into AMMs

Decentralization isn't a synecdoche

TL;DR Market makers in TradFi have always had privileges relative to standard traders. AMMs should follow this pattern, as the status quo is unsustainable.

Problem

Vertical integration substitutes a hierarchical governance mechanism for markets. In the case of automated market makers (AMMs), giving traders zero trading fees in exchange for a 90% profit tax would be no different than the typical hedge fund scenario where they give portfolio managers capital to let them keep 10% of their profit.

Currently, the most popular AMMs generate fees of only 5 bps for the LPs who bear all of the pool’s impermanent loss (IL). In comparison, front ends for Uniswap and ThorChain charge 25 bps or higher while bearing no direct operating expenses. AMM protocols take their money-losing LPs for granted.

Defi is based on Satoshi's principles of decentralization and permissionless access. While these are good things, it's important to remember these principles apply with nuance, as all principles do. Dapps can give traders special privileges yet still be decentralized and permissionless. A market is decentralized if there is open entry and exit, but all markets contain firms that involve hierarchies, where their employees have different rights and responsibilities, as opposed to every task farmed out for bid at Fiverr. The current inability of LPs to capture trading profits that CLOB market makers or Las Vegas bookies capture creates dead markets like those in Augur, where the bid-ask on probabilities was often 0.25-0.75. Unfortunately, the creator of Augur, Joey Krug, made a fortune despite its failure and now works with VCs that fund crypto protocols, ensuring the cycle repeats. Virtually no one in defi gives more than lip service to the parochial mechanism design configurations essential for sustainability.

Vertical integration overcomes the primary AMM deficiency by moving arbs from outside third parties to a more efficient relationship where they have rights and responsibilities. These privileged arbs are still decentralized because they are pseudonymous and uncensored, but they must interact via a contract that enforces a mutually beneficial quid pro quo.

Given that the arb’s job is straightforward and requires no specialized alpha, the profit made by arbs is not worth anything near what LPs are giving away to them. Protocol designers focus on their AMM's breadth of coin and chain coverage, UX, extensibility, and partnerships. Defi's brief history shows that the protocol token performance correlates little with LP profitability. The AMM developers lack of IL appreciation—if it's impermanent, it's irrelevant!—has resulted in AMM stagnation and the rise of centralized crypto exchanges like Bitmex, dYdX, and Hyperliquid.

Economic theorists commonly assume profits are zero in equilibrium, a simplifying assumption useful for analyzing the effects of supply and demand shocks. This zero-profit assumption is counterproductive when designing protocols. In the real world, risky investments require a profit to incent efficient decision-making at every level, and these profits often come from irreversible investments of uncertain imitability that create a moat for competitors. These investments include branding, supply chain networks, low-latency network connectivity, and legal or institutional fiat. Profits do not trend to zero in growing economies, nor should they, a fact economic theorists have rarely appreciated.

A problem with trading commodities or stock certificates is that these goods are perfect substitutes. A share of Apple stock is the same no matter who is selling it, so competition among suppliers with identical cost functions leads to zero profits, and the market breaks down. A sustainable market requires all participants to be better off when they play the game: consumer surplus for consumers and profit for suppliers. The New York Stock Exchange discovered early on that by restricting who could buy or sell securities, they could provide better liquidity, which enhanced the value of these securities. This ultimately led to specialists who had monopoly control of various stock listings. In the 1960s, the Nasdaq adopted a slight variant, the cartelized dealer market. Both gave market makers pricing power, allowing insiders to profit handsomely, especially given the standard regulatory capture that prohibited alternatives by fiat. A good thing was made into an ultimate thing, a common human error.

In the 1990s, the internet disrupted this equilibrium and decreased trading fees by 90% from 1990 to 2010. Electronic market makers have replaced an explicit specialist/dealer moat with a standard market moat created by the cost and complexity of creating a high-frequency trading system that relies on economies of scale to process many different assets. In markets where being a few milliseconds too slow is fatal, the natural power law distribution in ability prevents outsiders from sniping market maker profits down to zero (though current UChicago economists have a plan to fix that!).

Sadly, no AMMs present their LP returns net of their expected IL expense. Some AMMs present LP returns net of specific historical ILs, like the past month, but these metrics are so noisy everyone sees them as irrelevant. One cannot fix what one does not measure meaningfully, so, unsurprisingly, most defi innovations are focused on incentives that appeal to the gullible innumerate, like BLAST points and BLAST gold, increasing complexity with multiple tokens that act like multi-level marketing pyramids. Protocol incentives are a great way to extract house money from idiots who think they can front-run pump-and-dumps, but it is not a long-term solution for creating a sustainable market.

Solution

My solution focuses on the fact that for a decentralized AMM, its price will always follow centralized exchanges (CEXes). Any minimally decentralized validator set will be sufficiently geographically dispersed to make it an order of magnitude slower than a CEX, where high-frequency traders have co-located servers responding to trades within 10 milliseconds. This makes the arb's task trivial: push the AMM price to the CEX price whenever they deviate by more than 5 basis points. Empirically, this is what AMM arbitrageurs do, which is quite different from what most people imagine arbitrage to be: the two-legged arbitrage where one buys on one exchange and simultaneously sells on another. While two-legged arbitrage does happen, it's rare because it's simply too costly. Most arbitrageurs engage in ‘statistical arbitrage’ that generates the same profitability but relies on the law of large numbers.

The great benefit of an AMM arb over an oracle that updates the AMM price is that arbs do not present attack surfaces. Oracles can be hacked or manipulated. Regulators can and ultimately will regulate Chainlink if it ever services a sufficiently successful AMM, making them only useful for infant dapps. Arbs are pseudonymous, and even if regulators doxxed and persecuted one of them, new arbs will respond to the profit opportunity due to the permissionless nature of decentralized blockchains. Open and uncensored access is the key to decentralization.

How arbitrageur profits are related to IL

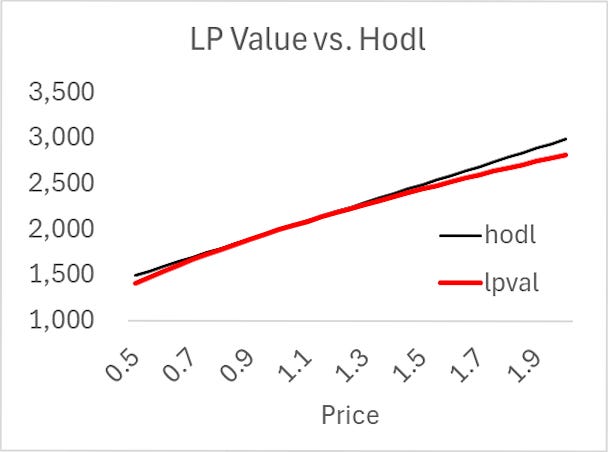
LP's net profit is its share of fee revenue minus the option expense they generates via their negatively convex position.

The LP's value in red contrasts with a base ‘hold-on-for-dear-life’ (Hodl) position in the asset. The LP's value is always less than or equal to the initial Hodl position set at the price of 1.0 above; its first derivative is positive, and its second negative. A negative second derivative is known as being negatively convex or having a negative gamma. The effect of negative convexity is the basis of countless articles published on options and other derivatives over the past 50 years since Black-Scholes, as true as the Pythagorean Theorem. This implies that the expected value of the LP position outside of fees is negative, and the longer the horizon is, the more likely it is that the LP position will be negative.

The LP's net profit is his fee revenue minus his convexity loss:

LP profit = volume*fee – IL

The LP's option expense can be amortized into a continuous expense (theta, lvr) or looked at episodically, like the IL from a particular start and end time. It's better to amortize it like theta because when IL is looked at historically over a particular period, you are extrapolating from a single observation with a large standard error. It's tempting to take an IL=0 over some horizon and comfort oneself that this loss is 'impermanent' and will return to zero as it has in prior times. This is a logical fallacy, like inferring that you do not need fire insurance because your house has never burnt down. The average of many (60+) daily ILs will approximate the expected IL, and these are convenient ways to measure IL, so I will refer to IL as something measurable that is always positive (i.e., it's an expense).

One definition of IL is the difference to the Hodl value:

IL = LpValuet – Hodlt

This can be rewritten as a function of the current price applied to the original (t=0) and current (t=1) LP position, updated to current prices.

Rearranging we get

Surprisingly, this precisely mirrors the cumulative effects of an arbitrageur updating the pool price to the CEX price:

The sum of the ArbitragePnLs applied continuously or once has the same expected value. The expected value of a price-setting arbitrageur without competition is the same whether the arb trades every minute or once a day. This is not obvious because when hedging frequently, the arbitrageur will make many offsetting trades that cancel out (see here for a proof).

The asset price determines the IL and its corresponding arb PnL, which has nothing to do with adverse selection. An AMM is like a CLOB in several ways, but the most significant difference is that its price only moves when there is a trade. To blame the arbitrageur for taking advantage of the AMM's stale price and then adverse selecting the AMM makes no sense, as pushing the AMM price to its true price is how they work. One could avoid the constant product AMM IL by creating a CLOB or frequent batch auctions. Still, these have their versions of IL and, more importantly, do not work well on decentralized blockchains where latency and transaction costs are orders of magnitude greater than in TradFi.

To intuit the arbPnL/IL equivalence, consider Bob's AMM, where Bob acts as both the LP and price-setting arbitrageur and charges a fee (e.g., 5 or 30 basis points). Bob creates an arb-bot that sends trades to set the AMM price at the CEX price.

Bob's LP profit = priceSettingVolume * fees – IL

Bob's Arb profit = IL – priceSettingVolume * fees

In this example, Bob's expense in one account is revenue in the other, and vice versa, so Bob's net profit is zero. Bob generates a Hodl return, and the pool price is always set to the CEX price.

Noise Trader vs. IL arbitrage

A noise trader pushes the price away from its equilibrium price, and the arbitrageur makes a profit pushing the AMM price back to its original price (back-running), often making only a couple of basis points.

Noise traders are uninformed only with respect to immediate small-scale price deviations between exchanges. These would include trades such as selling ETH to buy a Lambo, buying ETH because of an informed long-term investment thesis, and trading based on alpha delusion. Noise trades are random over the long run and are not biased toward pre-fee profit or loss. Over time, the net position acquired reversing noise trades sums to zero, making them valuable order flow liquidity providers target.

While price-setting arbitrage PnL mirrors the LP's IL, noise trading arbitrage mirrors the noise trader’s loss. To see this, consider the case where the price of token A is stable at $100.0. A noise trader sells 1 unit of A and pushes the AMM price down to $99.0 for a fill price of $99.5 (in AMMs the fill price is the mean of the start and end price). The arb buys 1 unit, which pushes the AMM price back to $100.0. Another noise trader pushes the price to $101.0 for a fill price of $100.5. The arb sells and pushes the price back to $100.0.

Example of Noise Trade Arbitrage

The net result for the noise trader, arb, and LP in the above table is zero change in their token positions. We can see the profits above without fees, where the noise trader loses $1, and the arb makes $1. If we add a fee of $0.1 for each trade, the LP would make $0.4, the arb would make $0.8, and the noise trader would lose $1.2. The net pool trader pnl (arb & noise) would be -$0.4 (+$0.8 - $1.2), and the LPs would net +$0.4. The noise trader fee revenue plus the arb fee revenue applied to noise trade reversals is pure profit to the LPs, unlike the price-setting arbitrage that exploits the LP's negative gamma. Thus, an active arb's gross profits will be at least as significant as the LP's IL, as it also includes noise trading arb profit.

The Ideal

An AMM needs LPs to supply tokens and arbs to keep the AMM price fresh. The arb's net profit subtracts the fees it pays to the pool.

Arb net Profit = (IL – priceSettingVolume *fee) + (noiseGrossProfit - arbNoiseReversingVolume*fee)

We can break out the LP's fee revenue into three sources: noise trader fees, the fees generated by arbs reversing noise trades, and arb price-setting trades when the CEX price moves. Bob made zero profit in the example above, where he is both the LP and arb, and there is no noise trading. Noise traders generate profit for LP via their fees and the fees generated by the arb reversing the noise trades. The LP's cost is the IL.

LPs Net Proft = noiseVolume*fee + arbNoiseReversingVolume * fee + priceSettingVolume *fee – IL

If we could combine the arb and LP profit, the arb's fees and IL would cancel out. The result would be a strictly positive number generated by the noise traders.

Arb + LP PnL = vol(noise)*fee + noiseGrossProfit

This is the ideal that can feed the arbs and LPs collectively, as noise traders are willing to pay to get access to a fair price. The practical question is, to what extent can we combine the LPs and arbs to make it easier for them both to generate a profit, as opposed to the status quo where only the AMM arbs profit?

Empirical AMM Profitability Data

For any pool, the volume is dominated by a handful of arbitrageurs who trade hundreds or thousands of times daily. By pulling the swap transactions and sorting by sender volume, the arbitrage addresses stick out under the top 3 addresses, and these contracts are private. In contrast, front ends offered by Uniswap, 0x, and 1Inch generate a significant amount of AMM trade, but these addresses link to verified contracts, which allows users to trust them.

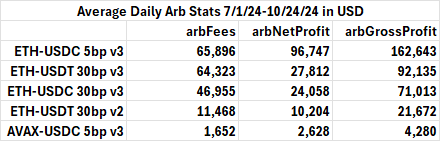
The table below shows the identified arb accounts generated between 45% and 76% of pool volume. All the Uniswap pools examined below traded USD stablecoin against either ETH or AVAX. Four were capital-efficient v3 pools, the other a v2 pool. The USDC-ETH mainnet 5bp fee v3 pool is the most popular AMM pool currently and historically (since May ‘21).

Stats on Pools Examined

Only the unrestrictive range v2 pool LPs generated a net profit. This can be seen below by looking at the pools's total fees compared to their expenses estimated via a daily LP PnL. Arb accounts make positive profits for all pools, and the arb and LP profit sum is always greater than zero.

If we transition arbs to a zero-fee regime, the amount of profit available to be taxed would be larger because the arb net profit above subtracted fees, and the new regime would eliminate those fees. The sum of the arb net PnL and the arb fees paid presents the amount possible to split between the arbs and LPs, the arb gross profit.

If the LPs captured 90% of the arb's gross profit and all the noise trading fees, they would cover their expense, the IL, in every pool. This is a lower bound because without fees, the relative advantage will allow the arbs to capture more of the LP’s IL, and more noise trading profits. In the table below, rev/expense greater than 1 means the LPs make a profit.

Of course, the immediate question is whether the arbs would still make a profit after being taxed 90%. Western economies have tried to set marginal tax rates at 90% over the past century, and they inevitably revert to 40-50% after encountering the downside of the Laffer Curve.

A better way to think of the arb is not as a citizen doing myriad things to make money who has to pay protection money to the state but as a portfolio manager within a hedge fund. Hedge funds often charge 2-and-20 to their clients: 2% of assets and 20% of profits. Yet within the fund are various portfolio managers (PMs), each with distinct strategies and segregated accounts. The typical PM takes between 5 and 15% of their profits (pre or post 2-and-20 depends on the HF). The individual PMs benefit from the trading infrastructure, accounting, legal, and, most importantly, the capital provided by the fund.

Lending tokens to Arbs

An AMM arb's task is easily automated into a program that monitors the relative AMM and CEX prices, and given knowledge of the pool's liquidity, the profit-maximizing trade parameters are straightforward. AMM arbs do not need the alpha TradFi requires because of a decentralized blockchain’s latency. The arb needs capital, however, and the cost of capital needs to be covered by the arb's profits. The LPs can significantly reduce the arb's capital requirement, turning the 90% tax into the attractive 10% take PMs accept at the hedge funds.

The pool can loan the tokens that arbs need for trading. This requires that the arb have an on-contract margin account tied to the AMM contract so the LPs can enforce their profit-sharing rule and prevent losses from potential arb insolvency. While an arb that perfectly captures the IL will never lose money, in practice, the arb can be reckless, malicious, or experience an anomalous market event. If the pool is lending the arb money, they need to ensure the arb's account is solvent; otherwise, their loss will have to be paid for by the LPs. To protect against this, the arb needs a required margin, and if the arb's margin is below the required amount, liquidators can seize the arb's tokens and exit his position before the pool loses money.

For example, consider the pool with moonCoin and USD, with 1k of each at an initial price of 1.00 USD. The table below shows how an AMM pool balances change when moonCoin's price halves or doubles (both equally likely). When the price of moonCoin declines, the pool acquires more moonCoin and loses USD. Instead of making the arb provide the moonCoin to move the price down from 1.0 to 0.5, the pool could lend their moonCoin to the arb, creating an asset for the pool, a debit for the arb. In the table below, the fact that at a price of 0.50 there are not 1414 moonCoin, but only 1000, is no different than in restricted-range v3 pools where LPs create virtual tokens to emulate the unrestricted v2 pools. The LP's position value and IL are unaffected by this accounting contrivance.

The corresponding arb's margin account would look like the blue table directly above. Note the required margin is considerably less than the net USD value of the tokens needed to generate these price movements on the pool. This is useful in estimating the arb's return on capital. I applied a required margin of 20% of the arb's risky asset position (5:1 leverage). While there have been several 20% intraday moves in BTC and ETH, they are rare enough not to be fatal via an insurance fund for such events. Once the arb's account value is less than his required margin, liquidators are incented to seize the account immediately. As such moves take at least 15 minutes, this should minimize losses from margin account insolvencies to tolerable levels.

When the arb exits, or just takes his profits, he must first pay off his entire debt. Thus, if the price fell from $1.0 to $0.5, he would have to pay off his entire moonCoin debt; if the price rose, he would pay off his entire USD debt before withdrawing anything. This ensures that the pool's real token balances equal its virtual token balances over time. Every arb liquidation or exit zeros out the amount lent to the arbs, ensuring the integrity of the pool.

If the price falls, the arb's profit is $86, and his 10% take means he gets to keep $8.6 ($9 w/ rounding). Thus, the other $77 goes to the LPs as part of their profit share. The LP's IL in this state thus reduces from $86 in the standard case to $9. On the doubling side, the IL is reduced from $172 to $17. The arb’s required margin if he exits with a moonCoin credit is irrelevant, as it will always be 20% of his moonCoin balance, so he will never be in danger of liquidation after exiting his positions while leaving money in his margin account.

Adding Noise Revenue

While the above shows how a profit tax can reduce the LP's IL, noise trader arbitrage can allow LPs to eliminate their IL entirely. To get an empirical sense of the magnitude of noise trading on AMM arb profits, I separated trades into whether they were the only pool trade in a block or occurred when there were other trades. Arb trades made with other trades in a single block are more likely to be reversing noise trades.

The table below shows the LP's net pnl from trades generated via arbs and non-arb traders, and in both singleton and multiple-trade blocks. The red numbers for the non-arbs imply they tend to lose money, which makes sense given zero edge and their fee. The arbs, in contrast, made profits in each scenario.

These profits were calculated using the end-of-day price, like having an end-of-day markout for each trade or assuming the traders hedged their positions at the end of every trading day. As the LP is on the opposite side of these trades, we see that the sum of the arbs and non-arbs in the singleton blocks generates strict losses for the LPs on singleton trades, which is dominated by arb trading.

The arb’s profit in multiple-traded blocks was relatively higher in the 5 bp fee pools than in the 30 bp fee pools, and their profits in the singleton blocks were significantly greater than those in the multiple blocks. This is for two reasons. First, there aren't many trades in the 30bp fee v3 pools. Secondly, the average non-arb trade's price impact is only around 4 bp, which will not generate frequent arb profit opportunities in a pool when the arbs must overcome a 30 bp fee.

Below, is a table of the gross arb profit across the pools in singleton and multiple-trade blocks. For the popular pools, noise trade arbitrage represents about 50 to 80% of gross profit if we assume all the singleton trades were price-setting, and all the multiple-trade blocks were noise trade arbitrage.

It seems likely that a prominent pool can generate decent returns for LPs on popular pools. For less liquid pools, the noise trader volume may not be sufficient to generate a decent LP return, especially if v3 LPs start to increase their leverage in response to higher returns. No market can generate profits assuming a large enough increase in supply; we just want to enable some pools, especially the most liquid ones, to generate LP profits.

Arb Return on Capital w/ 10% Profit Take

The arb's take is 10% of their gross profit, which is easy to measure. This will be less than their current profit, but the key is their return on capital. A relatively riskless return of 5% or 10% above the risk-free rate should be sufficient to incent someone to do the job, even if it is not the current arbs. The LPs do not 'owe' the current arbs anything, as they have been transferring wealth to them since May '21.

I used the average 7-day net USD traded by the arbs to estimate arb capital. Given 20% leverage, this would cover the required capital for a net USD amount traded 5 times the average, a decent worst-case scenario. If the arbs have that much capital applied, they might be capped out of trading a few days a year, in which case the AMM price would be set by those paying the entire fee, which is no different than today. The worst-case scenario for arbs would not be fatal for the AMM, and the effect on the arb’s expected return would be insignificant.

Divide the average daily PnL by the capital, multiply by 365, and get ROEs for the arbs above 29%+. The arb revenue is not riskless like a Tbill, but it is invariably positive over a month or two.

The status quo is not sustainable, let alone poised for flourishing. The current focus on gimmicks is pathetic, but it is understandable, given that TradFi is effectively barred from DeFi due to regulations. The guys who made a fortune on various failed protocols, meme coins, and NFTs funding AMM development, and all their expertise is in marketing and programming. All it takes is one AMM out there to adopt something like this, and they will dominate their competitors. Crypto needs decentralized AMMs, which won’t persist on money-losing LP capital. Without decentralized AMMs, crypto will have more choke points on centralized exchanges, enabling greater control by regulators protecting the fiat monopoly.