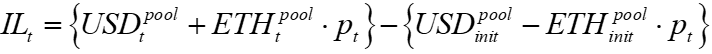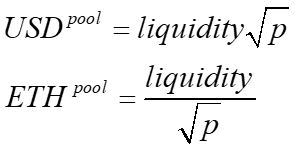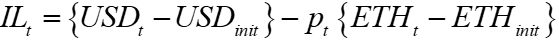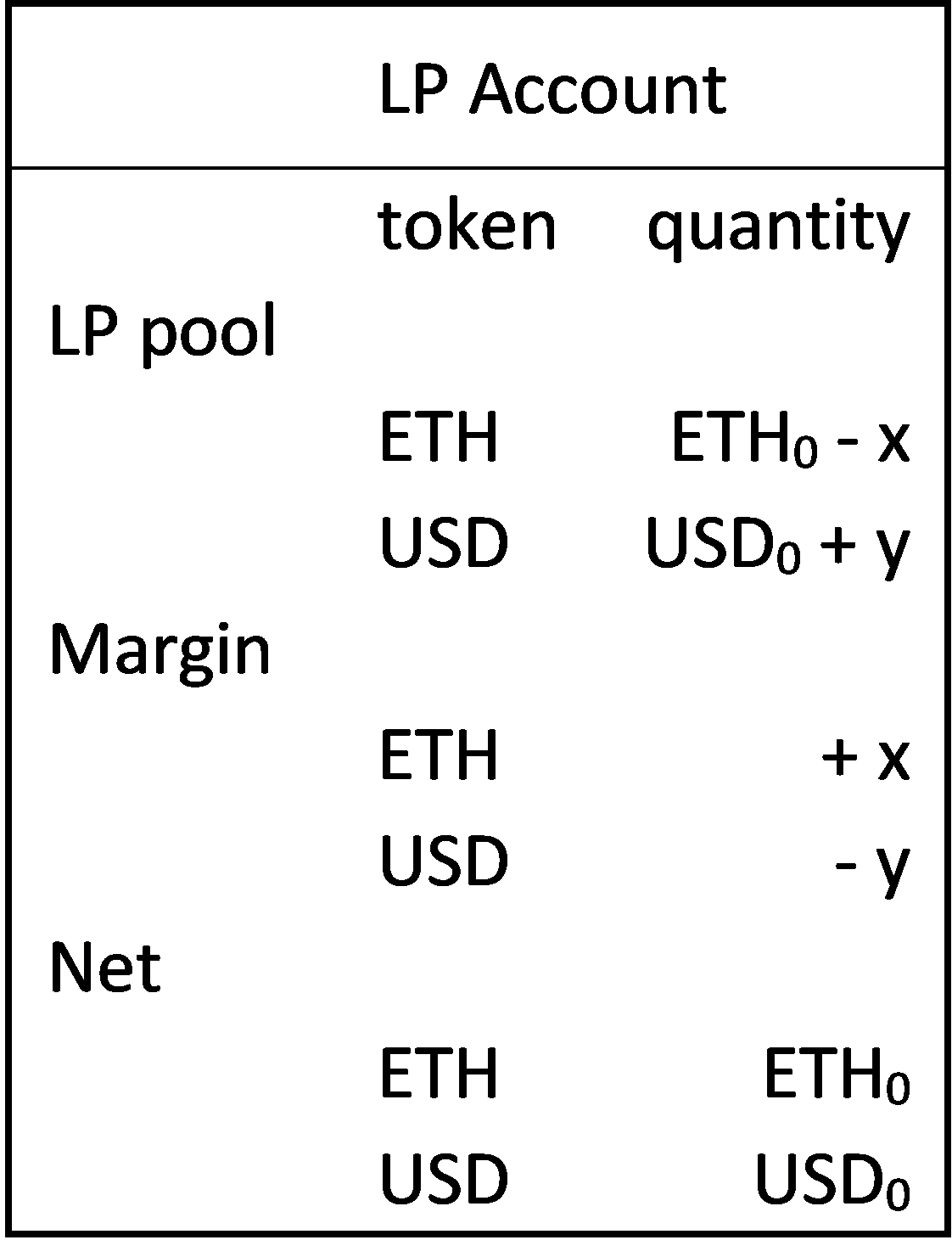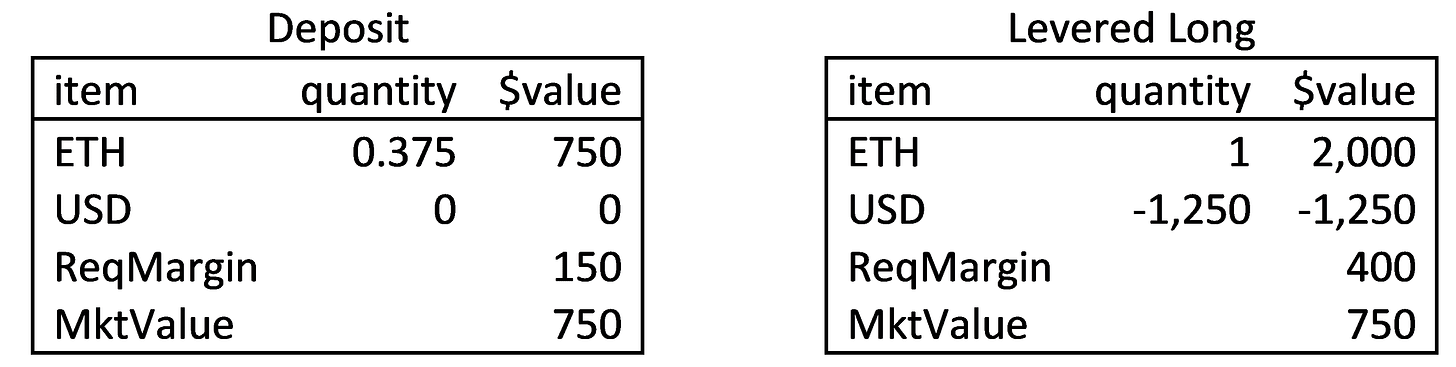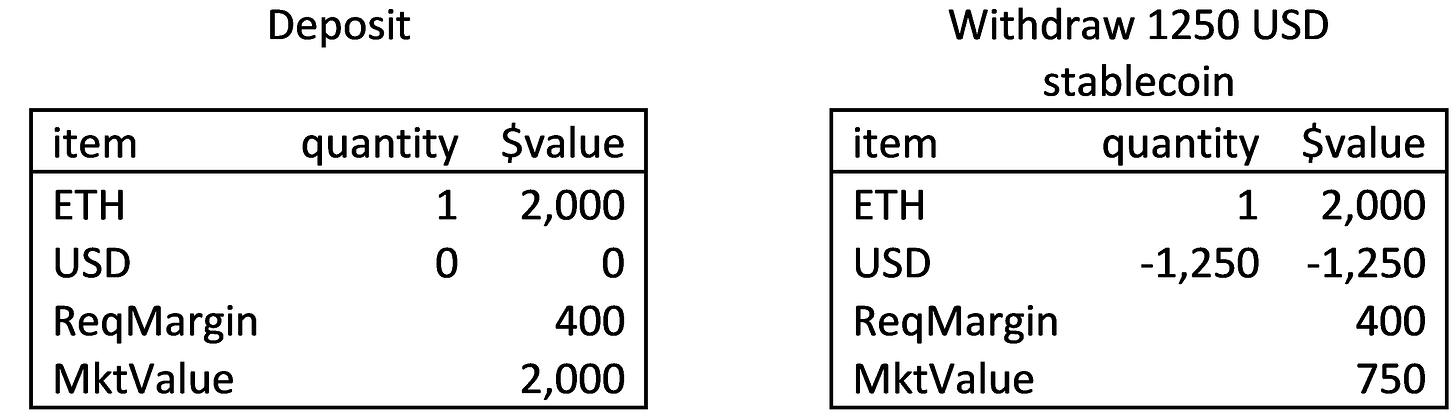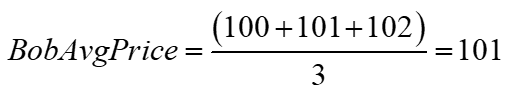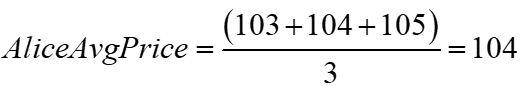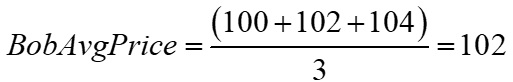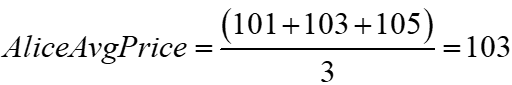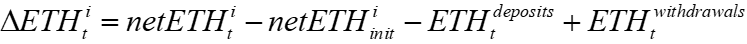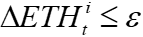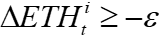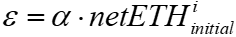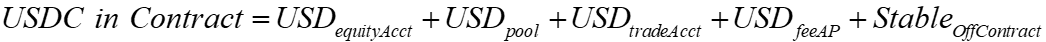A working prototype exists on the Avalanche testnet Fuji here, with links to the contract source code. Patent pending.
This paper describes a mechanism for eliminating the impermanent loss in a constant product Automated Market Maker (AMM) via a handful of contract refinements. These refinements facilitate several significant complimentary AMM efficiencies. The necessary LP margin extends in two important ways, which is why it is called a Leveraged AMM or LAMM. LP margining naturally extends to generate LP capital efficiency without restricted ranges; LP margin easily extends to allow traders to lever and short. Unlike perpetual swap markets, a LAMM does not require an oracle or financing rate to tie the LAMM price to the price on standard exchanges. A stablecoin naturally emerges from a margin account and can eventually create an uncensorable stablecoin. Finally, margined accounts imply a positive probability of account insolvency, giving LAMM equity capital in the contract an essential purpose as an insurance fund.
AMMs Unprofitable due to Impermanent Loss
The AMM removes conspicuous flaws in a blockchain CLOB by eliminating the need to adjust their limit orders continually. However, it still generates costs that need to be drastically reduced if this new exchange mechanism is to flourish. The loss experienced by AMM LPs is called ‘impermanent loss’ in the industry, hereafter IL, in the AMM literature.1 It is defined as
In equation (0.1) above, the initial bracket refers to the LP’s current pool value, as the quantities of an LP’s pool USD and ETH change with the price; the comparison portfolio is the LP’s initial pool token deposit at the current price. The LP’s initial USD and ETH deposit quantities are fixed, but the pool quantities vary via the following formulae.
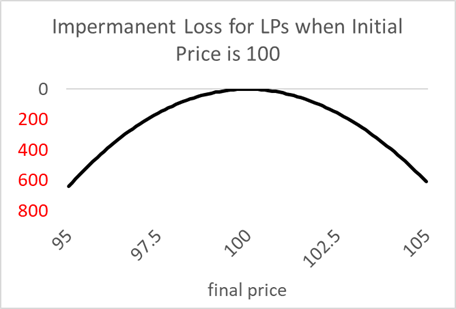
Equation (0.2) above is derived in the attached Appendix, but the gist is that it generates an LP expense that looks like a standard short straddle position, as in the graph below. It is concave (negative convexity) because the amounts are functions of the square root of p, and negative convexity implies an option expense. The IL can also be considered due to the adverse selection implicit in the constant product equation.2
This straightforward IL function allows us to estimate the LP’s option expense. The LP’s revenue is a fixed percentage (e.g., 0.05%, 1.0%) times the volume. Using the revenue and costs, we can document that the most popular AMM, Uniswaps ETH-USDC pools, lose money. See the Appendix or this post for documentation.
Volume on AMMS became significant in 2020, which was caused by and then accelerated the crypto bull market in 2020-21. Each month, tens of billions of USD worth of tokens are traded on these AMMs. However, volumes have declined, unlike the usage pattern for novel technologies like the internet or cell phones. Further, the volume has declined even on the newer layer 2 blockchain with much lower transaction costs. If LP losses are not rectified, these AMMs will disappear as a fundamental requirement for a sustainable game is that all participants generate a profit (the participation constraint in game theory).
Greater capital efficiency, lower latency, or equity token air-drops will not fix this.
IL Elimination Concept
The key to removing LP IL is to accept that an AMM will always be a derivative market to the traditional CLOB markets. The unique and novel AMM arose due to a decentralized blockchain’s order of magnitude difference in latency and gas costs (centralized exchanges have nothing comparable to gas cost).3 While AMMs work better than a CLOB on a blockchain, it does not work when it aspires to compete with CLOBs as a price-setting market. AMMs will always be the tail, not the dog. Some users may be discouraged by removing their delusional hope for an eventual dominating crypto exchange, in the way that online shopping eventually dominated mall shopping. However, many users will appreciate AMMs’ crypto virtues of permissionless access, transparency, immutability, and pseudonymity.4
If we accept that reality, the AMM has the perfect structure for creating a unique exchange where LPs are not subject to the standard ‘short straddle’ expense endemic to liquidity providers. For standard negative convexity exposures, hedging costs are unavoidable because practical experience has always been that the hedger responds to price changes in the underlying asset. This assumption is implicit in the Black-Scholes equation that equates the gamma term with the option premium. Hedging transforms the option expense implicit in negatively convex exposures by reducing its variance but not its expected value.
Thus, my approach applies a novel method based on an unappreciated property of the AMM that allows LPs to be the price setters. AMM users and researchers have applied the standard strategy that reacts to price changes, hoping that this new exchange technology, blockchain-based AMMs, will emulate and eventually replace CLOBs as the dominant mechanism to trade, thus setting the price of assets. However, a more modest appreciation of what AMMs can do—providing a mechanism to trade as a derivative exchange—highlights a dual-objective, price setting and hedging, that simultaneously eliminates the LP option expense.
It only works for the decentralized blockchain constant product AMM because decentralized blockchains’ latency and transaction costs are orders of magnitude greater than standard exchanges.5 This makes it possible for LPs to gain a dominant advantage when arbitraging the AMM (aka price setting).
In standard markets, the arbitrageurs develop algorithms that process an undefined information set, anything relevant to the economy or the asset, to estimate a target price. Distilling a predictable target price, even given access to high-frequency data, is not a straightforward objective. Those who can do it have 'alpha,' a skill that is by definition rare, so given the division of labor, market makers focus on skills more relevant to their role in the market, which is providing liquidity.
However, the 100-fold latency on blockchains transforms the arbitrageur’s difficult problem into an unambiguous target available to everyone: the current price on the major CLOB exchanges. These prices are generally within 0.05% of each other, and there is nothing comparable in statistical power available to those operating at the 5-millisecond timescale. The current CLOB price will be orders of magnitude more important than any other information statistically, so with modest effort, no one has an advantage or disadvantage when targeting a price (API link to big CLOBs ). A trader with a sizeable fee advantage (e.g., 0.3%) will have the ability and incentive to arbitrage the AMM price using the CLOB price.
Curiously, given the objective of providing liquidity at a derivative price, the AMM is more efficient than the CLOB. AMM math ties the LP’s token balances to the price as a precise function of liquidity. In contrast, on a CLOB, the market maker inventory is not necessarily related to price changes, and a market maker’s liquidity ‘size’ is ambiguous given the multidimensional nature of a market maker’s strategy (frequency of updates, queue or spread targeting, etc.). Any rule defining which LPs are hedging would be arbitrary and then gamed into irrelevancy, an application of Goodhart’s Law (‘When a measure becomes a target, it ceases to be a good measure’). In contrast, on an AMM, the clear position-price relationship as a function of liquidity makes it possible to identify hedging LPs, which is essential for limiting the arbitraging role to such agents.
Further, market maker adverse selection costs have been an outstanding problem for decades. One solution has been to give certain liquidity providers monopoly power, as in the old specialist system. Currently, market makers achieve monopoly power via the costly barriers to entry generated by regulations and the large capital investment needed to dominate the speed battles (e.g., the tunnel from New York to Chicago). For a derivative market, these are deadweight costs that decrease market efficiency.
The Math Behind Removing the IL
The impermanent loss (IL) is the difference between the LP’s current pool value and the value the combination of tokens would have had if it were not in the pool. Rearranging eq(0.1) we get the following
Equation (0.3) above shows that if the LPs keep their contract token amounts equal to their initial deposit amounts on the AMM, they will eliminate their impermanent loss. As the LP’s pool quantities move in opposite directions and are always positive, we need an additional set of LP balances on the contract so they can offset their pool position changes without having to deposit or withdraw tokens from the contract. These balances must allow for negative quantities so that LPs can offset pool token increases.
Necessary Mechanisms and Their Extensions
Margin Balances
With margined accounts, LPs can trade on the contract to offsets their pool position changes from a net account perspective. Below in Figure 5, we see how an LP buying x ETH for y USD keeps his initial token positions, ETH0 and USD0, unchanged.
Figure 5
LP with Netted Margin Account
Complement: LP Leverage and Capital Efficiency
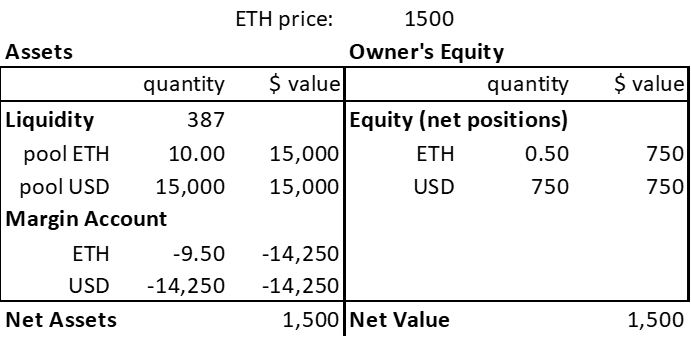
The leverage implicit in giving LP’s margin balances has the additional advantage of making the LP position more capital efficient. With margin accounts, we can leverage the LP pool positions by recording the borrowed tokens as negative quantities in the LP’s margin balances at the inception of an LP deposit. This generates similar capital efficiency to the restricted range approach that currently dominates AMMs but does not require updating one’s ranges as prices change. Figure 6 below shows an LP’s balances given a leverage of 20. (see Appendix for Capital Efficiency)
Figure 6
Leveraged AMM Accounting
Complement: Trader Leveraged Long and Short Positions
While this AMM provides the basic swapping of USD for ETH and vice versa, as in Uniswap, LP margin treatment naturally allows traders to lever long and go short by maintaining net positions on the contract, as in crypto perp exchanges. Initial trader deposits can be in USD or ETH to establish accounts, but they can sell tokens they do not have in their accounts by simply debiting their margin balances. This naked short selling works because the LPs are incented to have net positive balances of both tokens and as long as the LPs supplying the pool have net positive amounts of both tokens, a trade can happen. Further, the trade’s economic impact in the context of a solvent pool is the same whether or not the trader is selling short or an existing long position.
Figure 7 below shows the accounting effects when a trader levers long. Here the trader deposits 0.375 ETH to establish a long position in 1.0 ETH (here, we show a required margin of 20%). (see Appendix for more examples of margin trading)
Figure 7
Leveraged Long Trader
Complement: Stable Coin
A stablecoin also naturally arises, given margin treatment. Figure 8 below shows a user deposit who has deposited 1 ETH worth $2000, seen on the left. If that user withdraws 1250 USD as a USD stablecoin, the withdrawal debits the user’s USD balance. The account on the right is identical to the case above, though in that case the trader levered a long position with an ETH deposit. This highlights the natural extension of stablecoins within margined exchanges. It is the same balance sheet as in a MakerDao collateralized debt position used to create their stablecoin, DAI.
Figure 8
Stable Coin Account
It should be noted there is no money multiplier process as in fractional reserve banking because each account is over-collateralized. If all individual accounts have a positive net asset value on the contract, the contract is solvent, and the USD stablecoins created have as much value as a stablecoin in the ETH-USD pool (e.g., USDC or Tether). (see Appendix for how this can ultimately facilitate a decentralized stablecoin)
Implied New AMM Requirement: Liquidation Mechanism
In an account with margin treatment, the net asset value can become negative as asset prices change (e.g., in the case above, if the ETH price dropped to zero, the account would have a negative value). This implies a liquidation mechanism is needed to protect the contract from insolvent accounts that could lead to contract insolvency.
As with standard margin accounts, various liquidation rules have been applied to blockchain contracts. The trader’s net asset value must be above a required margin ratio (e.g., 20%) to avoid liquidation. Unlike other liquidation mechanisms for stablecoins, however, the contract allows for liquidation on the contract, as it is also a trading contract. Further, as the AMM’s price is tied to ETH’s true price via arbitrage, no oracle is needed to monitor account solvency, removing an attack surface for hackers. This is because a functioning AMM should have a clear arbitrage incentive to keep the AMM price at the true price. So a hacker who tries to push the AMM price from its true price to generate fraudulent margin violations will become a money pump for arbitrageurs if the LP arbitrage bots are functioning. (see Appendix on liquidation mechanics)
LPs get a Trading Fee Discount
The next refinement gives the LPs a trade fee discount to dominate arbitrage trading. As the AMM price changes only when the net trades are non-zero, a significant price change implies non-zero net trading. If the LPs set the price on the AMM, their net trades in their margin accounts will offset their pool position changes, generating zero net token changes for the LP’s net account. This relegates non-LP trades to net zero sizes, consistent with liquidity trading.
A market price equilibrates supply and demand. Informed traders compete at margins to anticipate the future market price by looking at qualitative information and correlated assets. Liquidity traders (aka ‘uninformed’ or ‘noise’ traders) buy and sell for other reasons, such as a need for cash to buy a car or because last weekend, they decided they would buy ETH. The net demand of these liquidity traders is zero because a market price equilibrates their buys and sells; this is why they are called noise traders, in that their demand is like white noise, a stochastic term with a zero mean.
It helps to see how those with a fee discount will dominate arbitrage and how arbitrage trading implies net trading demand equal to the LP pool position changes. Consider the following example. Assume a standard trading fee of 1.0% but a discounted fee of 0% for Bob. If the AMM ETH price is within 1.0% of the ‘true’ price, only Bob can profit by buying or selling ETH until the price on the AMM equals the true price. Non-LPs have no incentive to push the AMM to its true price because their cost, 1.0%, is necessarily greater than any potential profit they could make. Thus, if the LPs consistently keep the AMM price within 1% of the true price, non-LPs will transact for reasons unrelated to discrepancies between an AMM price and its true price. This is called ‘uninformed’ trading and does not mean without any information, just not information relevant to arbitrage or small, high-frequency price movements.
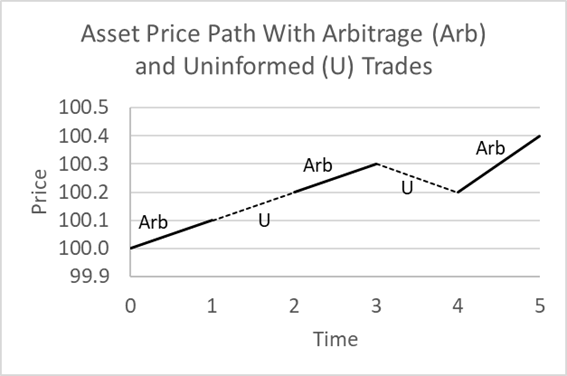
Figure 9
In Figure 9 above, we see a price path where the non-LP trade for uninformed reasons and the LP trades for arbitrage reasons. The price starts at 100.00, and the true price is immediately revealed to be 100.1. The LP buys, and the new price is 100.1. At the new price, an uninformed trader buys, pushing the price up to 100.2. Fortunately for that uninformed trader, the new true price is revealed as 100.3, and the LP buys and pushes the price to 100.3. The LP has bought about 2/3 of the total buys that have pushed the price to 100.3. The uninformed trader sells this time, pushing the price down to 100.2. Now the true price is revealed as 100.4, and the LP buys and pushes the price to 100.4. In all arbitrage trades, the net buys for the LP completely explain the asset price move from 100.0 to 100.4.
An equilibrium market price equilibrates uninformed supply and demand, which implies these trades have a net zero value. In the short run, traders without the trade fee discount will generate net token demand. Over time, however, these noise trader imbalances will cancel out and generate a net zero demand along a price path.
Restrictions on LP Trade Fee Discounts
In addition to the LP trading discount that allows them to dominate non-LPs in arbitrage trading, we need to prevent the quicker or more active LPs from dominating the slower LPs when setting the AMM price. The problem would be this. Suppose all LPs could trade at a discount at any time. In that case, one super-efficient LP with only 1% of the total pool liquidity could monopolize the arb trading, leaving the other 99% of LPs subject to the same arbitrage costs as before. We can do this by giving the LP a trade fee discount conditional on their net ETH position being not too much above (below) their initial net token position when they buy (sell). For example, an unconstrained speedy LP with only 1% of pool liquidity would accumulate a sizeable net token position increase as the AMM ETH price rises, as their pool position would only decrease by 1% of the purchases credited to their margin balance. Restricting the LP trade discount based on the LP’s current to initial net ETH ratio prevents this situation.
Restrictions on LP Removals
Finally, we must prevent an obvious tactic that would abuse this approach. The objective is to reduce the costs of LPs who provide genuine service for traders, providing liquidity, which means letting traders swap tokens using the pool of LP tokens. We must prevent or penalize LPs who remove liquidity too quickly, as otherwise, they could add liquidity, make their desired trade, and then remove liquidity. While the blockchain is slow, this refers to responding to information, not the ability to run transactions sequentially. If one knows a precise sequence of transactions one wants to make, these can be sent via a contract on the blockchain so that they occur in immediate succession and instantaneously. Such a tactic would give a trader discounted trading fees without providing liquidity to other traders, a clear violation of the intent of the LP trading discount.
Example Highlighting How LPs Can Eliminate Their IL
In these examples, we will ignore leverage, the accrual of fees, and gas costs charged by the blockchain. These issues distract the LP’s mechanism of eliminating his IL, as the logic presented applies without losing generality to those issues.
Case 0: Benchmark Basic AMM
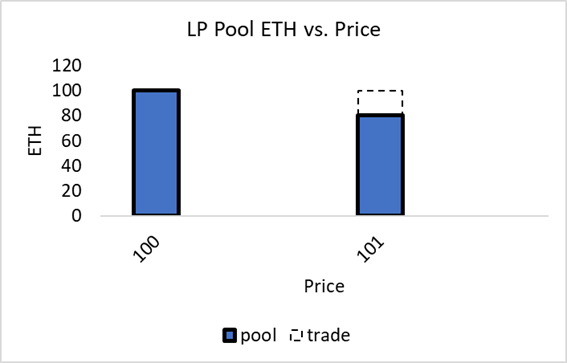
As a benchmark, consider the case where an LP supplies 100 ETH and 10,000 USD to the pool, reflecting an ETH price of $100. A trader buys ETH from the pool, pushing the price from $100 to $101. Buying ETH implies the pool sells ETH, so the pool ETH amount would decline, as in Figure 10 below, where the reduction in ETH from 100 to 80 reflects the 20 ETH bought by an external trader. In this case, the trader removes the ETH and makes an arbitrage profit, reflected in the LP’s loss, his IL, via Figure 2.
Figure 10
LP with no margin account
Case 1: 1 LP Trading with Self on AMM
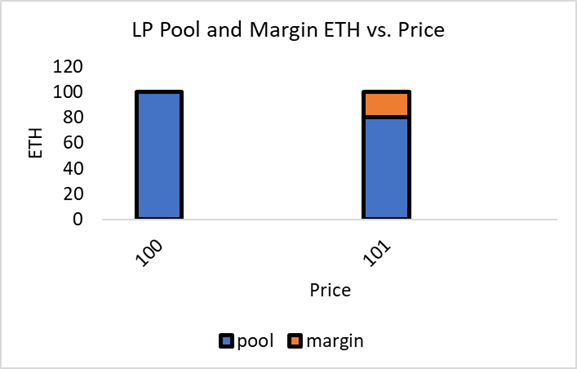
Now assume the LP has a margined account (no leverage applied as it would be an irrelevant distraction for these examples). In this contrived case, the LP, Bob, trades with himself on the contract. In this case, Bob’s ETH buy pushes the price up as before. However, unlike the base case above, the LPs net position does not change because Bob is both the LP and the arbitrage trader, and Bob’s trades are all on the contract. As the LP ETH decrease and trader ETH increase offset—he is just trading with himself—Bob’s net ETH position is constant at 100, though ETH moved from Bob’s pool account to his margin account. The arb’s profit offsets the LP’s loss, though these agents are just subaccounts within a singular account.
Figure 11
LP trades with Himself Using a Margin Account
A person trading with themself cannot make a positive or negative profit. If we assume the true price moved from 100 to $101, then the profit made by Bob’s arbitrage trading exactly offsets the loss that Bob’s LP IL made, so his account will see no net change in token balances, which implies a zero loss from a net account basis.
Case 2: Multiple LPs Trading
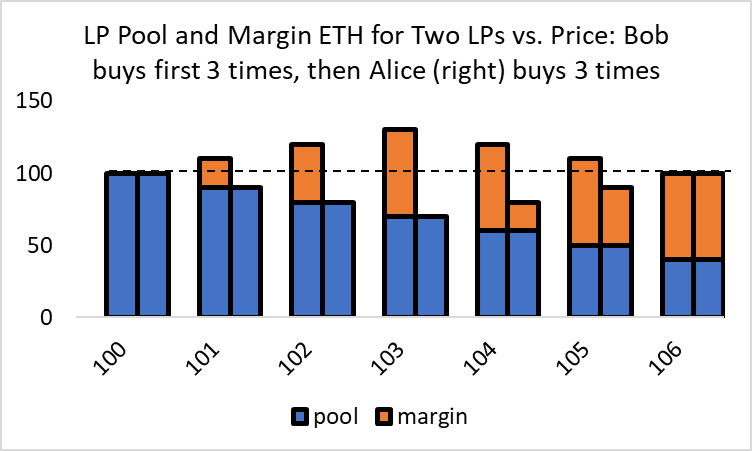
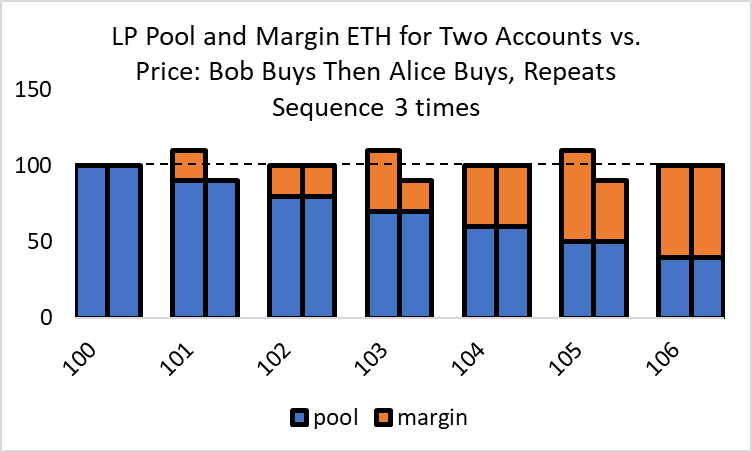
With more than one LP, a singular LP’s trades are spread across all LPs, which can generate significant IL among the other LPs. Consider the case where there are two LPs, Bob and Alice, each with identical ETH pool positions of 100. Adjacent columns reflect their initial pool ETH positions, Bob on the left and Alice on the right. Here Bob buys 20 ETH in three sequential trades, and the purchase amounts are stacked onto his pool ETH positions, reflecting his net ETH position. Bob and Alice have 50% of the pool, so each trade debits each LP by 10 ETH (1/2 times 20). Speedy Bob makes the first three buys in this price movement. His margin account increases by 60 ETH, but his pool account declines by only 30 ETH, for a net ETH balance of 130 ETH, an increase of 30 ETH. Alice, meanwhile, loses 30 ETH in her pool and net ETH and suffers IL.
Figure 12
Two LPs Trading, One Jumps in Front
If we stopped the price increase at 103, this situation would imply Alice is experiencing the same IL losses as if Bob were a non-LP trader, as in current AMMs.
Assume the price keeps rising, but Bob gets distracted playing League of Legends with his crypto-billionaire buddies. This allows Alice to rectify her ETH decline by making three sequential buys of 20 ETH, for a total of 60 ETH added to her margin account. These three trades do not affect Bob’s margin account balances but reduce his pool account by 30 ETH. The net ETH balance for both LPs is back to 100 but at a new higher price of 106.
While ultimately, the net ETH for both LPs is constant, we know their net USD positions, not presented here, are not. Bob bought his ETH at a starting price of 100, while Alice bought her ETH at a starting price of 103. These buys would debit the LP’s USD margin accounts, and Bob would have a smaller debit reflecting his lower purchase price. Their pool USD amounts would be the same because they have identical pool liquidity deposited at the same time and initial price. As Bob and Alice are the only traders and LPs on the contract, Bob’s net USD increase equals Alice’s USD decrease when she buys.
To see this more clearly, assume the fill price in USD per trade is the starting price for this example (an approximation that does not change the general result). Bob’s average cost was $101.
Alice’s average cost was $3 higher at $104, as she hedged only after Bob’s trades pushed the price up significantly.
Over large price changes, this could generate significant positive PnL for Bob, implying a significant negative PnL for Alice. While the IL for Alice is lower than if she did not trade and renovate her initial ETH pool position, her IL can still be significant.
Case 3: Multiple LPs Trading with Restrictions
As in Case 2, we have two LPs, Bob and Alice, with equal liquidity in the pool. This time, a restriction is applied so that Bob can no longer trade once Bob’s net ETH position rises above his initial net ETH position. Given the exact sequential price change as above, this allows Alice to start buying ETH at lower prices than in Case 2, even though an undistracted Bob would like to buy given the LP trade discount. That allows slower Alice to make the second buy in the price move sequence.
Figure 13
Two LPs Alternately Trading
Bob’s average cost is now $1 higher than in Case 2, as he trades at prices {100, 102, 104}, compared to {100, 101, 102} when Bob monopolized the first part of this price change in the example above.
Alice’s average cost is now $1 less than in Case 2, as she trades at prices {101, 103, 105}, compared to {103, 104, 105} when she could not trade ahead of Bob.
With the LP arbitrage trading restriction, we reduced the USD differential so that the average cost was only a $1 difference instead of $3. The specific numbers used in this simplified example are merely illustrative. More important is that it illustrates how restricting LP trading based on their net ETH position relative to their initial ETH position prevents subsets of LPs from dominating other LPs.
Summary of Methods Needed to Eliminate IL
1. LP accounts have margin and pool balances that are netted.
For an LP to maintain their net token amounts at constant levels, they need to be able to add or subtract to their contract token positions on the AMM contract without requiring deposits or withdrawals. Allowing LPs to margin trade allows them to buy and sell on the contract and maintain their net token positions, causing and reacting to AMM price changes that directly affect their pool balances.
2. LPs can trade at a reduced fee under certain conditions.
Define netETH(t,i) as the sum of the LP’s pool and margin ETH balances:
Define Delta-ETH(t,i) as the net trades made by LPi on the AMM via their margin account plus the change in the LP’s pool ETH. Any withdrawals and deposits after the LPs initial deposit of tokens should be subtracted from the LP’s initial net ETH balances so that this represents LP trades. If outside tokens could exogenously change their net ETH positions, the change in NetETH would not reflect trades on the AMM and thus effectively allow a speedy LRP to trade unconstrained and dominate the other LPs.
LPi can buy at a reduced fee if
LPi can sell at a reduced fee if
The limiting number e should be proportional to the initial LP net ETH deposit,
The buy and sell conditions are logically identical, reflecting the negative symmetry of buy and sell orders on the pool. In the example above, where Bob bought aggressively in front of Alice, we accumulated a large, and the implicit restriction on his trading after one trade is an example of applying rule 2. The LP reduced fee allows the LPs to dominate price setting; the restrictions on the reduced fee prevent more efficient or active LPs from dominating arbitrage and inflicting IL on the other LPs.
3. LPs must maintain positions for a minimum time.
Any removal of LP liquidity before a particular time horizon (e.g., one week) is prohibited. Alternatively, any removal of LP liquidity before a particular time horizon is charged a fee proportional to the liquidity amount to make this unprofitable.
This prevents a trader from getting the LP discount without effectively providing liquidity to traders, which would be blatant gaming of the intent of the trading discounts.
Equity Token Purpose
The equity balances in the account have two primary purposes. First, they provide an insurance fund for potential account insolvencies, a scenario not possible on standard AMMs, but common on stablecoin contracts like MakerDao or perp trading platforms. Second, as the equity account generates revenue from liquidations and trades, this aligns the incentives of the equity token holders with the users.
The equity token should have a modest governance function for straightforward upgrades, but the capital behind it provides a vital role as a cushion for potential losses on the contract. If one pays out equity only via redemption, it puts a floor on the token’s value at the contract’s net asset value, making the end-game wind-down straightforward.6 The equity fee is feasible instantly because, without the IL, the LPs can afford to give some of their fee revenue to the equity account. This prevents ‘mission creep’ built into the equity tokens that merely have vague governance rights, and users speculate on how it may be monetized in the future.
StableCoin Endgame
The LAMM provides the same swapping service on Uniswap, where users can execute a swap in one transaction. It can also give traders margin trading, allowing them to leverage and short. As the LPs are incented to keep their net token positions constant, there should always be always positive amounts of both tokens in the contract.
As the contract works even while accounts have negative margin balances for USD, and withdrawing USD from the contract generates a debit in their USD margin balance, a stablecoin representing a USD position has the same value as a USD credit on the contract. Account owners cannot double-spend withdrawn USD on the contract, and if they lose access to these stablecoins, the account will merely have a perpetual excess. There is no mechanism for anyone to access unclaimed assets within the contract.
The sum of all user USD balances, on and off contract, will equal the amount of the stablecoin used in the ETH-USD trading pair. This is because even if one deposits ETH to generate a stablecoin, one first must sell ETH to generate the USD balances that one can withdraw as the endogenous stablecoin.
Consider the initial case where there is a LAMM trading USDC and ETH. The initial deposits would be in USDC and ETH. Traders can withdraw a stablecoin from the contract, generating a debit in their margin balance.
Over time, additional LAMMs can be created with different USDC-Token pairs. Each LAMM would be independent and could have its own stablecoins. People could withdraw these stablecoins and create different stablecoin trading pools on Uniswap or via this mechanism. Over time, if the LAMMs functioned efficiently, people would come to trust the stablecoins from these different LAMMs.
Eventually, if the stablecoins generated were fungible into USDC, the stablecoins could then replace USDC as the USD base in the LAMMs.
In the long run, if the stables were accepted outside these LAMMs, there would be no need for USDC. To the extent the price of ETH is priced correctly in these LAMMs, they would be true stablecoins. With multiple robust LAMM using each other’s stablecoins and stablecoins having value outside the LAMMs, such as trading on independent AMMs, manipulating the various LAMM stablecoins simultaneously to defraud accounts in one LAMM would expose the manipulator to arbitrage, making the manipulator a money pump.
Conclusion
The benefits of the LAMM are not merely significant but necessary. Existing AMM LPs lose money after accounting for their IL expense, which is not sustainable. LP unprofitability has existed since AMMs began in 2020 and has shown no improvement. With a mechanism to give LPs a discounted fee, crafted so the LPs cannot abuse this privilege, the IL can be eliminated. This would promote a sustainable decentralized trading mechanism for tokens.
The margin needed for removing IL seamlessly generates two valuable features more efficiently via the complementary natures. First, it gives the LPs capital efficiency without requiring restricted ranges (see Appendix for detail). Currently, restricted ranges are 10 to 100 times more capital efficient, but they double the memory and CPU requirements for an AMM. This adds to gas costs and makes it more difficult to audit these contracts. Restricted ranges also require LPs to adjust their ranges over time frequently, and those who adjust less frequently will find their fee revenue diluted by more active LPs. A slower but moderately active LP in the LAMM can avoid revenue dilution from hyperactive LPs.
Another margin benefit is that it generates a superior perp trading platform. Existing perp markets have two conspicuous deficiencies. First, the funding rate is no longer needed as a ruse to give traders the perp price, which is tied to the spot price, in that users can trade a spot on the same exchange at the same price. Arbitrage will tie the perp price to the true price. Second, funding rates often require an oracle to generate a funding rate, and oracles present a hacking and censorship attack surface.
Additionally, the deception used by the price setters in perpetuating the financing fraud corrupts the insider’s ethics, leading to many costs that are impossible to measure. It would be naïve to expect the same group of price setters who manipulate the perp premium from not also manipulating users via front-running or pushing prices to force liquidations in volatile markets.
Lastly, margin trading facilitates a stablecoin and, ultimately, a completely decentralized stablecoin. The contract’s endogenous stablecoin has a trading platform with a price set by arbitrage, removing the need for an oracle used by MakerDao to assess collateral adequacy. Further, liquidations can occur on contract, removing the hacks surrounding auctions of accounts that have an insufficient margin.
Initially, an existing external stablecoin is needed to create a trusted exchange where the price is set by arbitrageurs who could trade the tokens on other accounts. Ultimately, however, with sufficient popularity and trust, the stablecoins created from various LAMMs could each feed each other so that tokens could trade at fiat prices without any regulatory attack surfaces.
If the price reverts to where it started, the loss will disappear, making it not necessarily permanent. However, such is the case for any unrealized loss, and such losses are rarely dismissed as merely ‘impermanent.’ The phrase stuck.
The IL here is a negative number, which can be confusing.
Gas fees are paid to miners, which would be like if CLOB market makers had to pay a dollar to internet administrators for each cancel and replacement limit order. A centralized blockchain, meanwhile, is fast but pointless.
As almost all retail arbitrageurs are deluded noise traders, prioritizing their interests is not a good business model, morally or economically.
A decentralized blockchain will not be centralized, so its worldwide distribution implies latency limited by the speed of light.
The endgame would be the ultimate wind-down. It is essential to have good end games because while they may be beyond notice initially, eventually, they come into view, and if this process is ad hoc, this generates a large attack surface. Reasoning backward, one does not want the prominence of an endgame to promote panic or hacks.